津田 一郎・田原 孝・岩永 浩明
(HOLOMCS Vol.3 No.4 (1992)
Capillary Chaos and its Significance in Information Processing
Ichiro Tsuda:Department of Artifician Intelligence, Kyusyu Institute of Technology lizuka,Fukuoka820
Takashi Tahara: Hizen National Mental Hospital Kanzaki, Saga842-01
Hiroaki Iwanaga: C&CR, Hakozaki 33-l3-l06, Fukuoka 812
(Received October l3,1992)
Abstract:We found a chaotic pulsation in finger capillary vessels in normal adults,psychiatric patients and newborn babies. Proof for the existence of chaos was provided by the reconstruction of the dynamics in phase space and the calculation of the Lyapunov exponents. From the aspect of chaotic information processing, we provided a measure of the information storage capacity of the observed chaos. This measure was also proposed to assure noninvasive access to the information system, namely the nervous system of the subjects. We also found a difference in the topology of capillary and cardiac chaos, and a difference in their dependence on the subjects’ conditions. Based on these findings, we propose new hypotheses for both the meta-boric and the autonomic nerve controls in humans.
要旨:この論文では、健常者、精神疾患患者、未熟児の指尖脈波においてわれわれが発見したカオスの特徴づけを行い、その生物学的および情報論的意味を考察する。いくつかの場合において指尖脈波と同時測定した、心臓の電位においてもカオスが観測される。指尖脈波も心臓電位も一変数の時系列として測定されるが、位相空間への埋め込みの手法を使うことによりデータの幾何学的表現が与えられる。これによりカオスかどうかの直感的判断が可能になる。実際、リアプノフ指数の計算はデータがカオスであることを示した。被験者の物理的及び心理的条件を変えると、指尖脈波のカオスのトポロジーとリアプノフ指数の値は敏感に変化した。このような状態依存性は心臓電位のカオスには見られなかった。このことから自律神総支配に関する仮脱を提唱する。さらに、得られたカオスの情報論的意味を考察する。この考察により、生体内で互いに相互作用しながら分散して存在するカオスプロセッサーが生体の動的維持に重要な役割を果たすというシナリオを描くことができる。
1.はじめに
動力学系の理論の最近の発展により、物理系だけでなく生物系においても複雑な現象を系統的に研究し、妥当な解釈を与えることができるようになった。特に実験データの有限次元あるいは無限次元空間への埋め込みの手法l) 2)はランダム現象の解析方法に新しい視点を与えた。すなわち、従来はあるランダム現象が与えられると、確率変数に対する分布を求め、さらに変数の平均値、分散などを求めるというのが常道であった。しかし、このような統計操作では現象の本質を必ずしも正確に抜き出せるとはかぎらない。実際、非線形系をあつかっていると、こういった統計操作によってその系を「理解した」と納得することはまずない。一方、カオス研究者が最初にその有効な使用方法を提唱して以来急速に普及したホイットニーの埋め込み定理は、ランダム現象に対するまったく新しい観点と理解に対する有効な方法論を提供した。すなわち、われわれはランダム現象を比較的小数自由度の力学に起源を発するものととらえ、力学系がその上で運動を行う不変な多様体の構造を抜き出すことで、ランダム現象の背後に隠された秩序構造を抜き出すように努める。
埋め込みの手法により、多くの複雑な系で決定輪的カオスの存在が明らかになった。特に、埋め込みの手法を使って、ヒトの脳波3) 5)や心臓の拍動6) 7)もカオス的であるという報告がなされ話題を呼んだ。この論文では、われわれは新しい「ヒトカオス」を明かにする。すなわちヒトの手の指の毛細血管におけるカオスである。
さらに動力学系の生物系への応用に関する最近の研究により、健康の回復過程の新しい指標の発見の期待が高まっている。適切な指標は治療と看護に使用可能である。循環器系においては末梢系は物理、心理条件に非常に敏感であることがわかっているので、末梢系のダイナミックスを再構築することでデータと制御条件の相関を研究することは価値のあることと考える。
ヒトの脳の重要な問題の一つは、心の状態の回復過程を測る指標をいかに抜き出すかである。これはケアーとリハビリテーションに結びつく。今回のわれわれの研究は精神病患者の回復過程の指標を発見するということによって動機づけられている。従って、末梢系を研究することは当を得ている。またこのような観点は精神病患者のケアーだけでなく健常者の日常的なヘルスケアーヘも応用可能である。
セルフケアーのこの基本的な考え方に動機づけられて、指の毛細血管にみられる脈波の時系列を測った。その結果、健常者と輔神病患者の両方にカオス的脈波を見いだした。末梢血圧を現す一変数の時系列データを力学系に埋め込むことでアトラクターの幾何学的表現をえるとともに、軌道不安定性の指標であるリアプノフ指数やアトラクターを備報プロセッサーと見たときの情報受容能力を評価することができた。幾何学、リアプノフ指数、情報受容能力の三つ組を「カオスの形」と呼ぶことにすると、この形は被験者の物理的及び心理的状態に依存する。それに対して、同時測定した心臓電位からえられたカオスの形は同様の条件の変化に対して鈍感であるか、または不変である。この発見は、自律神経支配に関するある仮説に導くとともに生体の動的維持に関する新しい概念をも導く。
なお、この総文は 8)Tsuda, Tahara, and Iwanaga, 1992をもとに書かれた。
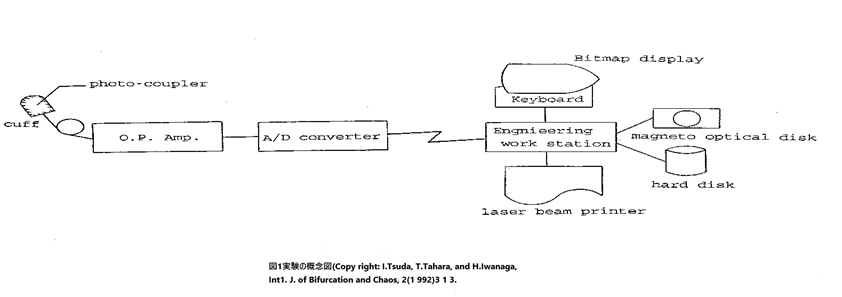
2.実験系
実験系の概略を図1に示す。ダイオード(LED)から発射された赤外線(940nm)の組織からの反射光を光トランジスタでとらえることで左手の人差し指の表面からデータをえた。測定点を固定するために発光部と受容部をカフのなかに装着し、カフの大きさを調節して適度な圧力が指にかかるようにした。組織で反射された光は光トランジスタによって電気信号に変換され、10,000倍された後A/Dコンバーターを通してワークステーションかパソコンに保存された。データはサンプリング周波数200Hz,12ビットの分解能で測定された。
Copy right: I. Tsuda, T. Tahara, and H. Iwanaga, Intl. J. of Bifurcation and Chaos, 2(1992) 313.
何人かの被験者でほかの指からの測定も行ったが、結果は親指以外は定性的には変わらなかった。左右差は若干認められたがそれほど大きな変化ではなかった。爪の表面からも同様の測定を行ったが、データの振幅が減少するだけであった。また、足の指からの測定も試みたが振動波形は得られなかった。
ここでの実験では、指の毛細血管中の血流量の約数ミリ四方における平均変動量を測定していることになると思われる。すなわち末梢血圧に相当する量が測られたと考えられる。
3.ダイナミックスの再構築
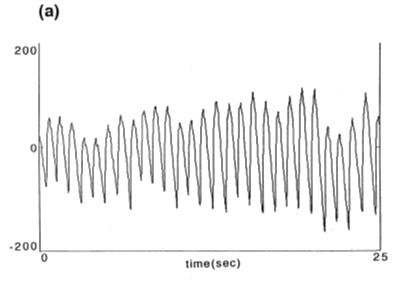
典型的な時系列を図2 (a)に示す。約1秒周期の振動が支配的である。この周期は心臓の拍動周期の影響である。しかしながら、もう少し長い観測時間では振幅、周期ともにかなりの変動を示す。われわれは約100秒間データを記録し、埋め込みの手法を使ってこの一変数時系列から現象の背後に潜む力学構造を抜き出した。
(Copy right: I. Tsuda, T. Tahara, and H. Iwanaga, Int. J. Bifurcation and Chaos, 2(1992) 313.)
(a)読書中のヒトの指先表面から計測された時系列(被験者 H. T.)。
数平方ミリメートルにわたる毛細血管の拍動の平均的な運動と考えられる。

(Copy right: I. Tsuda, T. Tahara, and H. Iwanaga, Int. J. Bifurcation and Chaos, 2(1992) 313.)
(b)四次元埋め込みにおける三次元平行投影図。
視線、\(n=\left(\frac{3}{4},\ \frac{1}{4},\ \frac{1}{4},\ \sqrt{\frac{5}{4}}\right)\)。
変数 \(w(t)\) の値が大きいほど軌道は明るく(白っぽく)描かれている。
背景はこの表現を示している。
(Copy right: I. Tsuda, T. Tahara, and H. Iwanaga, Int. J. Bifurcation and Chaos, 2(1992) 313.)
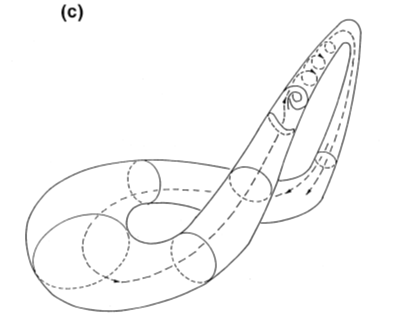
(c)指尖脈波カオスのトポロジーに対するモデル。
ここでは、末梢血圧の時系列 \(x(t)\) に対して、新しい独立変数として \(y(t)=x(t+\tau), z(t)=x(t+2\tau), w(t)=x(t+3\tau), \ldots\) 等を選ぶ。ここで \(\tau\) は適当に相関が残る時間間隔とする。時系列の三次元位相空間への埋め込みでは整合性のあるトポロジーは得られなかったので、四次元位相空間 \((x(t), y(t), z(t), w(t))\) への埋め込みを行った。図2(b)は一例である。四次元軌道を式(1)により三次元に平行投影し、変数 \(w\) が大きな値をとるほど明るい線で表示してある。
\begin {eqnarray}
\begin{array}{l}
\displaystyle x'(t)=n_2 \frac{x(t)}{A}-n_1 \frac{y(t)}{A} \\
\displaystyle y'(t)=n_1n_2 \frac{x(t)}{AB}+n_2n_3 \frac{y(t)}{AB}-A \frac{z(t)}{B} \tag{1} \\
\displaystyle z'(t)=n_1n_4 \frac{x(t)}{B}+n_2n_4 \frac{y(t)}{B}+n_3n_4 \frac{z(t)}{B}-Bw(t)
\end{array}
\end{eqnarray}
ただし、\(A=\left({n_1}^2+{n_2}^2\right)^\frac{1}{2}\ ,\ \ B=\left(1-{n_4}^2\right)^\frac{1}{2}\) で \(n=(n_1,\ n_2,\ \ n_3,\ \ n_4)\) は視線方向を表現する単位ベクトルである。四番目の軸 \(w\) はこの単位ベクトルの方向に一致するように回転される。
図2(c)は再構築された軌道の束(たぶんアトラクター)の骨格である。これは三次元トーラスの三次元ポアンカレ写像を想定して描かれている。指尖脈波の変動は主に、心臓の拍動、呼吸、血圧変化がそれぞれ非整合的な周波数をもって振動し、かつそれらの間に非線形相互作用が存在するためにおこる変動であると考えることは合理的である。したがって、ルエル・ターケンスの定理9)により、トーラス運動が不安定化しストレンジアトラクターが出現する。
4.カオスの実際的な指標:リアプノフ指数
再構築されたアトラクターは、その軌道が訪れる場所に片寄りがあるという意味において非・一様であるので、グラスバーガー・プロカチア法10)11)のようなアトラクターの次元測定法は適用できない。さらに、かりに次元測定が適用できたとして、非整数次元(フラクタル次元)が得られたとしても、そのことがただちにカオスの存在を意味するわけではない。いわゆるビンクノイズやレヴィー・フライトのような確率過程に従う軌道の集合体が非整数次元をもつことはマンデルブローによって徹底的に究明されたことであり、実際彼の先駆的なエッセイ12)のなかにはそのような例のコレクションが紹介されている。
リアプノフ指数は軌道不安定性(近くにある軌道が時間の指数関数で拡大する性質)の指標であり、その正値によってカオスの実際的な指標とし得る。しかしながら、実験データがカオス力学系に従うかどうかは原理的には決定不能問題であり、リアプノフ指数によっても実験データがカオスかどうかの判定には原理的な困難が伴う。たとえば、十分安定なりミットサイクル(散逸力学系における周期振動状態)にノイズが加わったような場合は、リアプノフスペクトルに正の成分が現れることはないのでカオスと区別できるが、リミットサイクルの軌道上のある方向に対して特に安定性に違いが生じる場合や、興奮的な系(サドルと安定固定点が非常に接近して存在するために、外部からの摂動により軌道が大きくはずれて弧を描きもとの固定点に戻るような系)に定常的にノイズが加わった場合は、リアプノフ指数は正の値として評価され得る。さらに、そもそも実験データを何次元の位相空間に埋め込むかはたいへん大きな問題である。アトラクターに一様性が保証できれば、次元測定を行い、あらかじめ何次元に埋め込むべきかは決定できるが、そうでない場合は決定できない。現段階においては、真のカオスと正のリアプノフ数によって特徴づけられる現象とを区別する整合的な方法はない。従って、あくまでその区別は経験的にならざるを得ない。
われわれは主にリアプノフ指数を実験データから計算することによって、カオスかどうかの実際的な判定を行ったが、推論を補強するために次元測定も行った。次元測定では標準偏差が非常に大きくなるのがふつうであるので、あくまで目安としてのみ使った。リアプノフ指数が安定に計算できなくなる度合いは最大リアプノフ数で最も小さい。我々は主に最大リアプノフ指数に注目する。計算結果は正の指数の存在を示している。すなわち、カオスの存在を示している。計算はウォルフ法13)を改良して行った。計算が正しく行われているかどうかの一つのチェックとしてローレンツアトラクターにこの方法を適用した。第一リアプノフ数は正しい値に2~3桁の精度で一致した。第二リアブノフ数は本来ゼロになるべきところが、0.003±0.0097であった。さらにわれわれは結果を確認するために、佐野-沢田法14)、エツクマンールエル法15)でも計算した。最大リアプノフ指数に関してはおおむね一致した結果を得たが、第二リアブノフ指数に関してはゼロか正かの判定は非常に困難でこの計算だけからはどちらともいえない。いずれの方法にしても、接空間をうまく張れたかどうかがポイントになる。
ウォルフ法での結果は四次元アトラクターに関する仮定を裏付けている。そこで、あまりあてにならないが、次元測定も試みた。典型的な例(図2)において、おおよそ2.9±0.5という値を得た。以上の計算および推論から、指尖脈波のデータは三次元もしくは四次元のカオスと判定できるが、少なくとも三個の脈波成分が関与していると考えられるので、おそらく四次元位相空間に埋め込まれたカオスであると考えるのが妥当である。
5.観測されたカオスの状態依存性
観測されたカオスの状態依存性を、健常者、精神病患者、未熟児において調べた。ただし、さまざまな物理、心理条件の変化は健常者についてのみ被験者が苦痛を感じないレベルで調べ、精神病患者については、安静平常時のみで測定し、未熟児に関しては集中治療室内で保育器に入っている状態と出たときの状態のみ調べた。
以下示すアトラクターの図はすべて同一の視点で描かれており、それぞれのシリーズで同一スケールの窓内で描かれているので、アトラクターの形状変化はデータの定性的変化を意味すると考えてよい。図3 (a)は健常者K.M .の脈波カオスで、左からそれぞれ、安静状態、非験者の興味のないテキストを読んでいる状態、被験者が興味を持っているストーリーコミックを読んでいる状態、コンピューター画面に突如現れたカラフルな動物の絵を見ている状態、のカオスの様子である。図3 (b)は健常者T.T.の左からそれぞれ、安静時、疲れた(と被験者が強く感じている)状態、アルコールを小量飲んだ直後の状態、のカオスである。
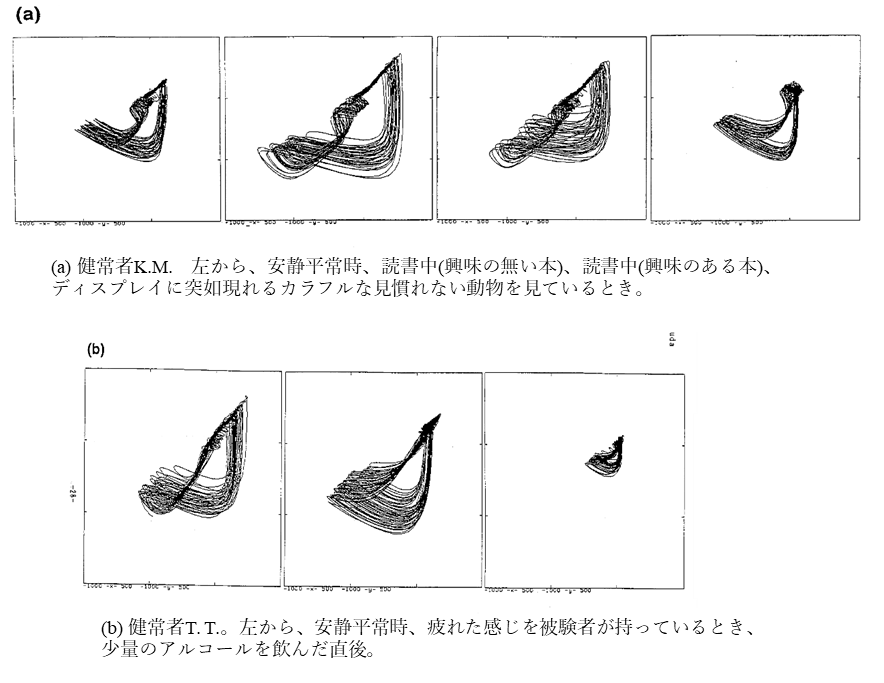
視線は図2と同じ。それぞれの被験者に対し、スケールはすべて同一
(Copy right: I. Tsuda, T. Tahara, and H. Iwanaga, Intl. J. of Bifurcation and Chaos, 2(1992) 313)。
次章で示すが、心臓に何らかの障害をもつひとの指尖脈波カオスは特徴的な乱れ方をする。また、一側性の軽い脳溢血(本人は少し偏頭痛があるという以上の自覚症状はなかったし、現在もほとんど自覚症状はない。また、日常生活も支障なく行っている。)をもつ人の脈波カオスは左手と右手ではっきりと異なっている、というようなことも分かるようになってきた。これらの例は、軽い異常が体内で発生したときに、われわれの方法を使うことで、簡単に異常の存在を判定できる可能性を示すもので、医学的にもきわめて重要な知見であると考えられる。そこで、もっと多くの例で研究したいのだが、都合のよい人が必ずしもすぐに見つかるわけではないので、この点に関しては系統的な研究ができない状態である。もしも読者の中で、お心当たりの方、もしくはそのような方をご存知の方はお知らせいただきたい。
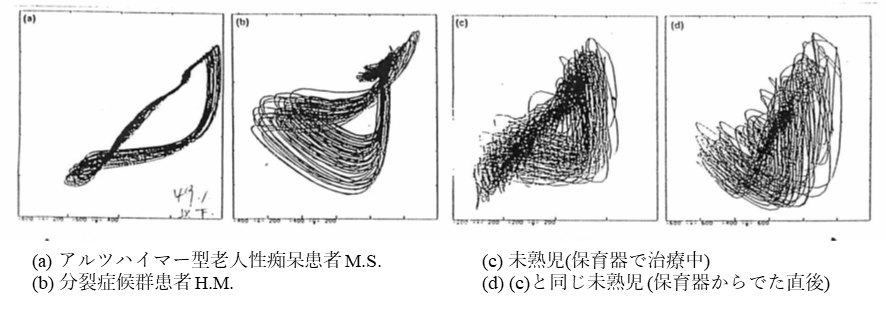
図4(a)は老人性痴呆患者M.S .のものである。非常に特徴的なのはカオス性がたいへん弱くなり、一つの周期成分が支配的になっていることである。実際、最大リアプノフ指数は小さい正数であり、第二リアプノフ指数はゼロである。このパターンは老人性痴呆患者に特徴的なものである。これが、痴呆からくるものか、血管壁の老化からくるものかは即断できない。図4(b)は分裂症候群に属するH.M.のものである。一般に分裂症候群の患者に特徴的なパターンは特に存在しないように思われる。実際、健常者と同様に第二リアプノフ指数までが精度内で正である。図4(c) (d)は集中治療室に入っている新生未熟児のデータである。(c)はまだ保育器に入っているときのもので、(d)は保育器から出た直後のものである。前者でははっきりしなかった構造が後者では少しできかかっている。実際、前者のリアプノフ指数はゼロであり、ノイズと区別がつかないが、後者ではリアプノフ指数はわずかに正の値となる。
(Copy right: I. Tsuda, T. Tahara, and H. Iwanaga, Intl. J. of Bifurcation and Chaos, 2(1992) 313)
このように、指尖脈波に現れるカオスの特徴は人の成熟度合いに関係している可能性もある。少し大胆な仮説として、次のようにいうことができるかも知れない。「赤ん坊の指尖脈波は基本的に無構造であり、はじめはカオスというよりノイズに近い。成熟するにつれ構造化が進み比較的次元の低いカオスになる。最大、構造化が進んだところではほぼ四次元位相空間に埋め込まれたトーラス崩壊後のカオスである。健康度が落ちる、もしくは老化が進むとカオス度が落ちてアトラクターの構造が単純になり周期状態に近づく。周期椛造だけになればそれは死を意味する。
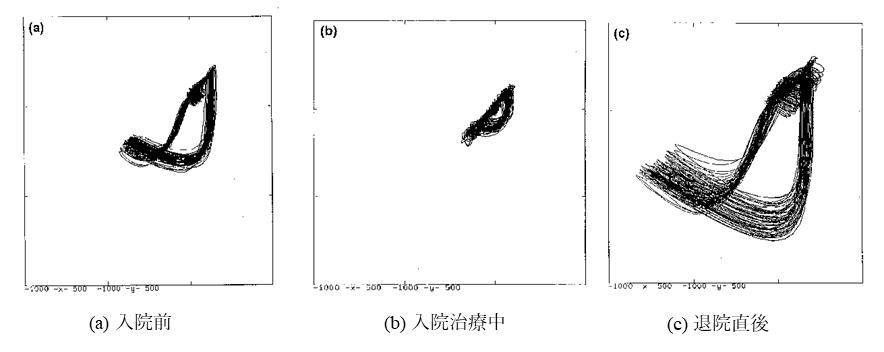
重要なことは、このようなアトラクター表現が物理的、もしくは心理的な病のケアーの過程におけるよい指標になるかも知れないということである。実際、われわれはこのことを確かめるために、軽い神経症患者の回復過程でアトラクターがどの様に変化するかを調べた。神経症患者S.S. に関するデータを図5に示す。図5(a)は入院直後の医学的治療を施す前の状態である。図5(b)は入院中のアトラクタであるがアトラクタのサイズが小さくなり乱れが目立っている。これは、投薬の効果かも知れないし、治療行為を通じての精神的葛藤の結果かもしれない。図5(c)は回復後、退院時のものでありカオスアトラクターの複雑な構造が非常にはっきりと表れている。
(Copy right: I. Tsuda, T. Tahara, and H. Iwanaga, Intl. J. of Bifurcation and Chaos, 2(1992) 313)
読者のなかには、われわれが物理的変化と心理的変化を混同して議論しているという批判を持つ人もいるかも知れない。しかし逆にわれわれがここまで見てきたことは、ヒトにおいては物理過程と心理過程はそれほど明確には分離されないという考え方を支持しているように思われる。特にその混合過程は末梢において顕著である。
6.心臓電位にみられるカオス
脈波カオスは大まかには心臓の拍動に近い周期をもつ。そこで、どの程度心臓の影響を受けているかは興味深い問題である。心臓の拍動の時間間隔がカオスであるということはすでに知られている。われわれは脈波と心臓電位の同時測定を行った。心臓電位はさまざまな測り方があるが、ここではV4誘導による結果を示す。われわれは現在までに確立されているすべての誘導で測定した。誘導によってはアトラクターの形状が多少異なっているものがあるが、基本的なトポロジーに変化はないように思われた。
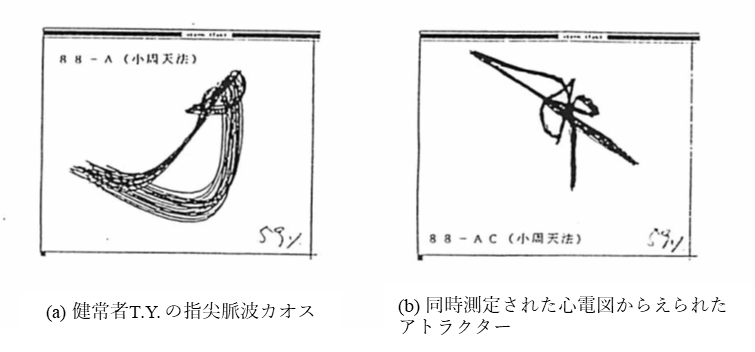
図6は心臓に欠陥がなくほかの病気もないと診断された健常者K.M.の心臓電位のアトラクター表現である(このときのK.M.の脈波カオスは図3 (a)の- -番左のパターンとほとんど変わらない)。図7には別の健常者T.Y.の脈波カオス(a)と同時測定された心臓電位(b)のアトラクターが示されている。KM.とT.Y.の脈波カオスには違いがみられるが心臓電位は両者でほとんど同じである。

(Copy right: I. Tsuda, T. Tahara, and H. Iwanaga, Intl. J. of Bifurcation and Chaos, 2(1992) 313.)
心臓電位にみられるこのようなアトラクターのリアプノフ指数も計算した。アトラクターの変化が激しいところが多いため、計算はかなり困難で、計算のために必要なふたつの参照軌道を十分長い間とることはできない。切れ切れの軌道で計算せざるを得なかったので、計算結果は正しいリアプノフ指数とは考えられない。むしろ、局所的な平均拡大率とみなければならないだろう。図6や図7 (b)のパターンの第一局所平均拡大率は正であった。第二局所平均拡大率は計算できなかった。しかし、健常者の心臓拍動の時間間隔がカオスであるという報告と照らし合わせて、図6,図7 (b)のアトラクターもカオスと考えて良いのではないかと思われる。
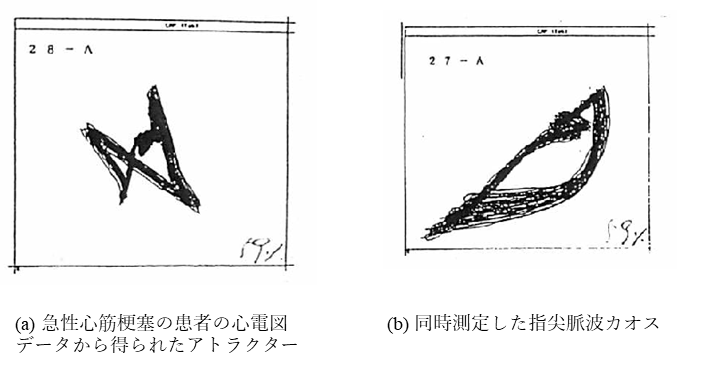
図8は心房細動の患者の心電図のアトラクター表現を示した。また、図9(a)は急性心筋梗塞の患者の心電図のアトラククタターー表現、(b)は同時測定した指尖脈波のアトラクターである。図6-9を比較すると、一見して心臓電位のアトラクター表現は心臓の異常の性質をよく反省していることが分かる。また図9より、心臓の以上は指尖脈波にも敏感に反映していることが明かである。
一般に、指尖脈波カオスは個人の健康度を反映するが、心臓電位のカオスは疾患を表現すると考えられる。
7.脈波カオスによる情報処理
循環器系は神経系と同様、情報チャンネルである16)。特に、循環器末梢系は神紙系と相関をもつ制御系と考えられる。従って、ここでえられたカオスの情報受容能力、すなわち入力された情報に対する受容能力、あるいは伝送能力を調べることは価値のあることである。カオスの情報受容能力を相互情報量で測る。カオス系と入力系の方程式が知られているときは、計算方式は確立されている17)18)19)。しかし、今回のように実験データに対して相互情報量を測り、情報受容能力を評価するには新たな工夫が必要となる。
\(\{x(n)\}\) をM次元ベクトル空間における \(n\) 番目の軌道点とする。\(M\) 次元位相空間へのデータの埋め込みによりこの割当は可能となる。\(\{y(n)\}\) を \(M’\) 次元ベクトル空間におけるほかのデータセットの \(n\) 番目の軌道点とする。\(\{y(n)\}\) は力学系の計算機シミュレーションでえられたか、あるいはほかの実験でえられたかであるとする。\(\{x(n)\},\{y(n)\}\)ともに力学の発展の順番に番号づけられている。次のタイプの強制系を考えよう。
\begin{eqnarray}
\begin{array}{l}
x(t+1)=f(x(t))+Cy(t), \tag{2} \\
y(t+1)=h(y(t)).
\end{array}
\end{eqnarray}
ここで、\(C\) は結合定数 \(c_{ij} (i=1, 2, \cdots, M; j=1, 2, \cdots, M’ )\)の行列である。
すべての \(i, j\) に対して \(c_{ij}=0\) のときの式(2)の解は \(\{x(n)\}, \{y(n)\}\quad (i=1 \leqq n \leqq N)\)を与える。われわれの目的は式(2)の解に近い時系列 \(x’ (n)\) を構成することである。\(x’(1)\) に対して \(x(1)\) を選ぶ。各ステップで \(f(x'(n)) +Cy(n)\) を使って \(x’ (n)\) からの正確な発展を計算したい。しかしながら、\(f\) の効果はデータセット\(\{x(n)\}\) の要素に対してのみ知られているので、このセットのなかの最近傍点を探すことで正確な発展を置き換える。
手続きは次のようなものである。
\begin{eqnarray}
\begin{array}{l}
x'(1)=x(1), \\ \tag{3}
x'(n+1)=x(k).
\end{array}
\end{eqnarray}
ここで、\(x(k)\) は \(\| f(x'(n))+Cy(n) \cdot x(k)\| = \underset{1 \leq l \leq N}{min}\|f(x'(n)+cy(n) \cdot x(l)\|\) を満たす。
次に、\(\{x'(n)\}, \{y(n)\}\) を \(m\) 個の細胞に分割する。\(\{x(n)\}\) が \(i\) 番目の細胞にはいる確率を\(p_i(i=1, \cdots, m)\) とし、\(\{y(n)\}\) が時刻 \(k\) で \(j\) 番目の細胞に入ったとき \(\{x'(n)\}\) が時刻 \(k+t\) で \(i\) 番目の細胞に入る条件付き確率を \(p_{ij}(t) (i=1, \cdots, m; j=1, \cdots, m)\) とする。このとき、時間付き相互情報量を次のように定義する。
\begin{eqnarray}
l(t)=-\sum_{i=1}^{m}p_i \log{p_i}+\sum_{j=1}^{m} \sum_{i=1}^{m}p_i p_{ji}(t) \log{p_{ji}}(t) \tag{4}
\end{eqnarray}
この量はふたつのデータセット\(\{x'(n)\}\), \(\{y(n)\}\) の間に共有された情報の時間発展を与える。今の場合結合が一方向なので、\(\{y(n)\}\) から\(\{x'(n)\}\) へ伝送された情報の時間発展である。
もっとも簡単な場合として、\(c_{kl}=c\delta_{kl}\)、ただし \(c\) は定数で、定常碓率、条件付き確率は\(\{x’(n)\}\), \(\{y(n)\}\) の第一成分のみで計算される場合についての計算結果を示す。まず、アルゴリズム(3)が良い結果を与えるかどうかを確かめるため、ローレンツカオスによって強制されたローレンツカオスに対して、ふたつの方法で式(4)を計算して比較した。ふたつの方法とは、方程式から時間発展を決める方法と、アルゴリズム(3)によって時間発展を決める方法である。計算された系は次に与えられる。
\begin{eqnarray}
\begin{array}{l}
\displaystyle \frac{dx_1}{dt}=-\sigma_1 x_1+\sigma_1 x_2+cy_1 \\ \tag{5}
\displaystyle \frac{dx_2}{dt}=-x_2+r_1 x_1-x_1 x_3\\
\displaystyle \frac{dx_3}{dt}=-b_1x_3+x_1 x_2\\
\displaystyle \frac{dy_1}{dt}=-\sigma_2 y_1+\sigma_2 y_2\\
\displaystyle \frac{dy_2}{dt}=-y_2+r_2 y_1-y_1 y_3\\
\displaystyle \frac{dy_3}{dt}=-b_{2} y_{3}+y_{1} y_{2}
\end{array}
\end{eqnarray}
ここで、\(\sigma_1=\sigma_2=10, r_1=r_2=28, b_1=b_2=8/3\) である。
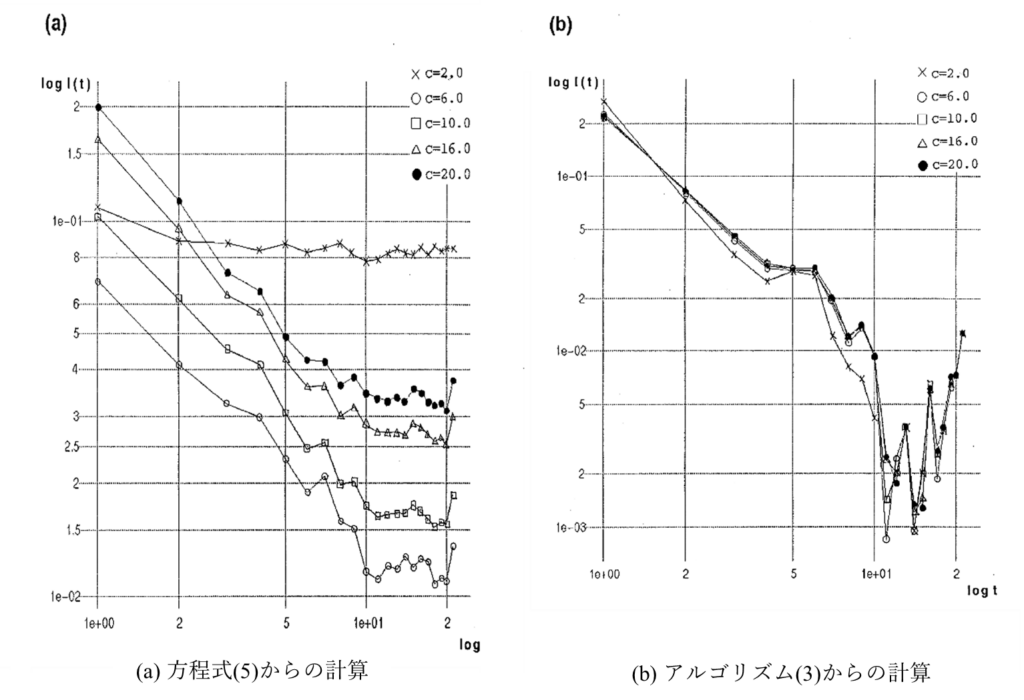
結果は図10に示される。(a)は方程式から求めた時間発展で計算した結果で、(b)はアルゴリズム(3)から求めた時間発展で計算した結果である。図では両対数で結果が示されているが、(a),(b)ともに直線的な変化を示し、傾きもほぼ一致している。(a)では、結合定数があまり小さくなければ(\(c=2\) を除いて)直線の傾きはほぼ一致している。これは、ある程度結合定数が大きくなれば、伝送された情報の減衰は時間を対数スケールで測ったとき一定の割合を保ち、その割合は結合定数の大きさには依存しないことを意味する。また、結合定数が大きいほど、初期に伝送される情報量は大きいことがわかる。これらのことから、カオスカ学系の結合により情報チャンネルがつくられると考えて、結合定数の大きさはチャンネルの大きさ、つまり伝送速度を決めており、減衰の割合はカオス固有の量で情報混合の割合であることがわかる。(b)では、結合定数によらず初期情報の値が同じであるが、これはアルゴリズム(3)のもつ弱点を表している。つまり、いまのアルゴリズムでは、もとのデータセットの順列を変えたもので摂動後のデータセットを代替しており、本質的に新しいデータは加えられていない。従って、結合定数の大きさによらない伝送速度が見かけ上得られてしまう。
(Copy right: I. Tsuda, T. Tahara, and H. Iwanaga, 1nt1. J. of Bifurcation and Chaos, 2(1992)313.)
ここでは、実験から得られたカオスの情報受容能力に興味がある。情報受容能力は、相互情報量の時間減衰の仕方で決まることがわかっている18)。線形減衰の性質を持つカオスは外部情報の受容能力は一般に低いが、指数減衰やべき減衰のカオスの受容能力は高い。ここでは、情報量の時間に対する傾きにのみ興味がある。図10に示された定性的な一致はアルゴリズム(3)が今の目的に限り有効であることを示している。
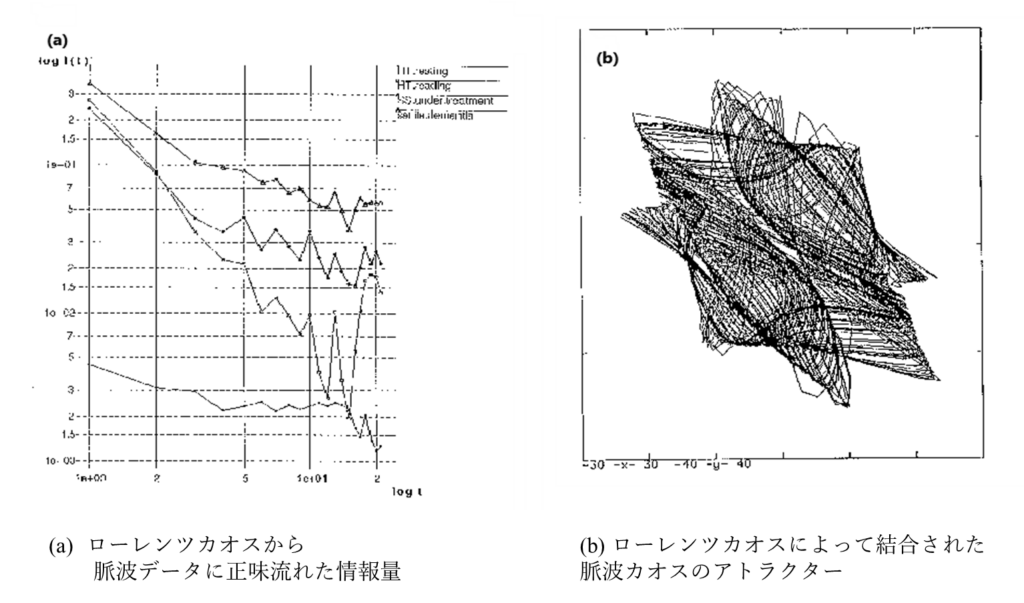
そこで、結合定数を固定して、実験データにアルゴリズム(3)を適用した。いくつかの結果を図11(a)に示す。あくまで、これはローレンツカオスの情報がどの程度各データに流れたかを示しているので、データの絶対的な情報受容能力ではない。ローレンツカオスに相対的な受容能力である。図11(b)にローレンツカオスによって摂動を受けたH.T.readingのカオスの埋め込み図を示した。
(Copy right: I. Tsuda, T. Tahara, and H. Iwanaga, 1nt1. J. of Bifurcation and Chaos, 2 (1992) 313.)
データの示す情報受容能力の高さは、このようなカオスデータが高次の情報処理のプロセッサーであることを示している。このようなカオスのネットワークは任意の外部情報をその振る舞いの中に動的に保持することができる17) 20) 21)。またこのようなカオスがネットワーク内に生成されると、パターンのすばやい非線形分離、学習能力の向上、二重学習(学習することを学習する22))のメタファーになりうる挙動などの性質が得られる23)。
8.提案と議論
前章で示した方法はデータとデータの間に流れた情報量の測定にも有効である。実際、われわれはさまざまなデータの間の情報の流れを調べ、興味深い予備的結果を得ている。このようにして測られた情報量はデータ間のコミュニケーションの度合いを調べる基礎になるので、これにより、データコミュニティーの中でのコミュニケーションネットワークを構成できるであろう。
もしも得られたデータがその人の情報代表系と考えてよいならば、この試みは非常に大きな意義と危険性を持ち得る。今回のわれわれの測定方法は無侵襲で、簡便であるところに特徴がある。ヒトの情報系に介入するいくつかの方法がある。まず、通常の会話を通してわれわれは他人の情報系に介入する。しかしこの方法はあまり洗練されていない。他人の情報系がどの様なもので、どの程度介入できたかを正確に知る尺度は存在しない。われわれは会話を楽しみ他者と自己を互いに啓発し充実させることはできるが、尺度の不在はこの方法の限界を暖昧なままにする。従って、科学的でない。コンピューターによるメールシステムも現在の状況では通常の会話と区別できない。コンピューターが受け付ける会話自体に極度の制限がもうけられるなら、関与する情報系の境界をコントロールできるだろう。しかし、現在のシステムはどんな情報も素通りしてしまうので、通常会話と本質は変わらない。次に、直接ヒトの脳に電極を差し込むことで情報系に介入するというやり方が存在する。しかし、これは倫理的な問題もあり、現実的でない。最後に残る方法は、ヒトの情報系を敏感に反映するデータを無侵襲で計測し、そのデータをヒトの情報系の代表系と考え、データに介入することでヒトの情報系に介入したとみなす方法である。実際われわれがここで試みたのはまさにこの方法である。
しかし、この方法には非常に大きな問題点がある。得られたデータがどの様な意味でヒトの情報系の代表系であるかがわからないので、データの意味を論じることは常に制限を伴う。特に深い意味を論じることは危険である。このような方法が有効になるためには、データ測定時の条件がコントロールされなければならない。またもし、データがある種の情報系の代表系であることがわかったとして、それにより、ヒトの情報系が部分的にせよ他人にあからさまにわかることは人権の問題に発展する。すでに現実に、ヒトのDNAというデータをヒトのある種の情報代表系と考えようという試みがなされている。部分データを管理することでヒトの情報系が管理される時代は確実にやってくるであろう。情報代表系を適切に選択し、それをどう使うかが科学的に議論されなければならない。
さらにこのような方法はわれわれの世界との関わりにある種の反省を迫ることになろう。データによるヒトの情報系への介入は、観測者が観測すべき系の内部にいるとしたときに発生する物理的な状況を再び想起させる。このようないわゆるEndoの世界では物理法則は観測者と対象との相対運動によってしか決めることはできない24) 25) 26)。われわれは観測による摂動無しの純粋客観の世界を知ることはできないのか、つまり世界の外にいる‘大いなる目’を持つことはできないのか、ということは深刻な問題になってきている。量子力学、カオス、ゲーデルの不完全性定理によって科学の問題として指摘されてきたことが、テクノロジーの発達による世界の時空の縮小と摂動効果の拡大により、非常に身近な問題になってきている。環境問題もこのような問題の一例である。自身が影響を与える世界の内部にいてなおかつ摂動を最小にできるような世界とのインターフェイスは存在するか。このようなインターフェイスが見つかれば、われわれは世界のなかにいながらにして、外の立場をとることができる。データによる情報系への介入というアイデアは、このような意味のインターフェイスの研究に貢献するだろう。
われわれの今回の研究結果から、循環器系と神経系の相互作用系に関する仮説をふたつ提唱する。心臓と指尖脈波のデータは異なるトポロジーをもつアトラクターを示した。両系ともに自律神経支配を受けており、脊髄から直接コントロールを受けている。従来、このふたつの系のコントロール系は同種であると信じられてきたが、われわれの結果は、両系のコントロール系は明らかに異なっていることを示している。さらに、心臓電位の示すカオスは心理、物理条件の違いによりほとんど変化しないのに対して、脈波カオスはそれらに敏感に反応し変化した。ここで、注意してほしいのは、心臓の拍動リズムは、たとえば緊張の度合いや運動状態によって大きく変化するが、電位のアトラクターの形はほとんど変化しないということである。このことから、自律神経支配に可塑性の点から二種類あると考えるのが妥当である。脊髄に二種類のチャンネルが存在し、一方は大脳からの神経結合が可塑的であり、他方は固定的でより自律的である。可塑的結合が学習型シナプスであるかどうかはわからないが、大脳の情報処理のあり方に敏感なチャンネルが存在すると考える。これが第一の仮説である8)。
第二の仮説8)は、得られたデータがことごとくカオスを示し、カオス度が健康状態に応じて変化していることから導かれる。生体においてはカオスの状態が定常状態であり、いわゆる、変化しない、あるいは周期的、という意味の恒常性(ホメオスタシス)はむしろ生体にとっての異常な状態ではないか。比較的制御された次元の低いカオス状態を恒常的に保つことのほうが、外界と情報的に遮断されないで生体を動的に安定化できると考えられる。このことをホメオダイナミックス、あるいはホメオカオス、という言葉ではっきりと表現しようというのである。
ホメオスタシスというのは文字どおりには、静的な状態を保つということだが、このことばが使われ始めた頃はむしろ、生体はもっとダイナミックで動的な協調性があるのだという含意があった27)。この含意をもっと積極的にさらに、カオスのもつ意味的重要性を考慮して、きちんと表現し直そうというのである。このような試みはわれわれだけに限らない。イベラルやイェーツは生体の持つダイナミックな応答性をホメオキネシスといっている28) 29)。レスラーは代謝系のカオス的な応答に着目し、カオス的維持という言い方をしている30)。またゴールドバーガーは心臓の拍動にみられるカオスが心筋梗塞の危機的状況で完全な周期状態に移行することを観測し、ホメオダイナミックスという言い方を提唱した。さらに金子と池上はかれらのケーム論的ネットワークにおいて、突然変異率の変化を高く保つ(孤立系では低い方が安定)状態がネットワーク内に安定にできるときに、比較的次元の低いカオス状態に自然に移行することを観測し、その状態をホメオカオスと表現した31)。
われわれは生体にとってカオスは本質的な意味があると考えてきた。今までは、おもに脳神経系や、認知心理的なレベルでカオスが重要な役割を果たしているという考えとモデル計算の結果を発表してきた20) 21) 23) 32) 33) 39) 35) 36)。今回の発見は循環器系でのものであるが、神経系、精神状態と密接に結びついたレ ベルのものであり、われわれの以前の考えを補強し、拡大する貴重なものであると考えている。
また、新しい考えがつけ加わった。そもそもこの研究は精神医療の現場から持ち込まれた問題意識に端を発している。すなわち、ケアーとキュアーという問題であある。時に、精神医療においてはケアーという概念がことさら重要であり、患者の自律を促すとともに、患者と共こあるケアーが模索されている。これは看護する側の自立を促すことでもある。従って、医療現場では、病気とは、健康とは、看護とは、治療とは、といった問題が日常的に実践を通して考察されている。カオスの概念はこのような現場に新たな考えを持ち込むだろう。精神医療の現場では、ケアーされる者とケアーする者が一つの系を構成するとともに、ケアーする者が‘大いなる目’を取り戻すことができるインターフェースを見つけなくてはならない。われわれのデータの測定法とデータの情報系への介入方法はこのような必要なインターフェースの目安となるかも知れない。生体からえられたカオスの意義は、ケアーする者に、自身が巻き込まれた系の記述不可能性と動的自律性の意味するところのものを教えてくれるという点にこそ存在するだろう。
参考文献
- N. H・Packard, J・P. Crutchfield, J. D. Farmer and R. S. Shaw, ”Geometry from a time series” , Phys・Rev. Lett. 45(1980)712.
- F. Takens, “Detecting strange attractors in turbulence” , Lecture Notes in Mathematics, 898 (1 98 1) 366.
- A. Babloyantz, ”Evidence of chaotic dynamics of brain activity during the sleep cycle”, in Dimension and Entropies in Chaotic Systems (ed. G Mayer-Kress, Springer, Berlin, 1986) 241.
- S. P. Layne, G. Mayer-Kress, and J. Holzfuss, “Problems associated with dimensional analysis of electroencephalogram data” , in Dimension and Entropies in Chaotic Systems (ed. G. Mayer-Kress, Springer, Berlin, 1986) 246.
- P.E. Rapp, “Dynamics of brain electrical activity”, Brain Topography, 2 (1989) 99.
- A. Babloyantz and A. Destexhe, “Is a normal heart a periodic oscillator?”, Biological Cybernetics 58 (1988) 203.
- H.L. Goldberger, D.R.Rigney,J.Mietus,E.M. Antman, and S. Greenwald, ”Nonlinear dynamics in sudden cardiac death syndrome: Heart rate oscillations and bifurcations‘’, Experientia, 44(1988) 983.
- I. Tsuda, T. Tahara, and H. Iwanaga, ”Chaotic pulsation in human capillary vessels and its dependence on mental and physical conditions”, International Journal of Bifurcation and Chaos, 2 (1992) 313.
- D. Ruelle and F. Takens, “On the nature of turbulence”, Commun. Math. Phys、20 (1971) 167.
- P. Grassberger and I. Procaccia, “Characterization of strange attractors, Phys. Rev. Lett. 50 (1983) 346.
- P. Grassberger and I. Procaccia, “Measuring the strangeness of strange attractors”, Physica D9 (1983) 189.
- B. B. Mandelbrot, Fractals-Form, Chance and Dimension(Freeman, 1977).
- A. Wolf, J. B. Swift, H. L. Swinney, and J. A. Vastano, “Determining Lyapunov exponents from a time series”, Physica D16 (1985) 285.
- M. Sano and Y. Sawada, “Measurement of the Lyapunov spectrum from a chaotic time series”, Phys. Rev. Lett. 55 (1985) 1082.
- J. P. Eckman, S. O. Kamphorst, D. Ruelle, and S. Ciliberto, “Lyapunov exponents from time series”, Phys. Rev. A34 (1986)4971.
- A. J. Mandell, “Dynamical complexity and pathological order in the cardiac monitoring problem”, Physica 27D(1987)235.
- K. Matsumoto and I. Tsuda, ”Information theoretical approach to noisy dynamics”, J. Phys. A: Math. Gen. 1 8(1985) 3561.
- K. Matsumoto and I. Tsuda, “Extended information in one dimensional maps”, Physica 26D(1987)347.
- K. Matsumoto and I. Tsuda, “Calculation of information flow rate from mutual information”, J. Phys. A: Math. Gen、21(1988)1405.
- I. Tsuda, “Chaotic itinerancy as a dynamical basis of Hermeneutics in brain and mind”, World Futures 32(1991)167.
- I. Tsuda, “Dynamic link of memory- chaotic memory map in nonequilibrium neural networks”, Neural Networks 5(1992)313.
- G. Bateson, Steps to An Ecology of Mind(Chandler Publishing Company, 1972)
- I. Tsuda, “Chaotic Hermeneutics for Understanding Brain ” , in Endophysics -the world from within(eds, G. Xampis, O. E. Roessler, and P. Weibel, to be published in l992)
- R. J. Boscovich, ”A theory of natural philosophy” (Reprinted by MIT press, 1 966, Original Italian version-1758, Venice)
- D. Finkelstein, “Holistic method in quantum logic” , in Quantum theory and the structures of time and space(eds L. Castell et al., Carl Hanser, Munich, 1 979)37.
- 26)0. E. Roessler, “Endophysics”, In Real Brains and Artificial Minds(eds., J. L. Casti and A. Karlqvist, North-Holland, New York, 1987)25.
- 島田一平(私信)
- A. S. Iberall, Amer. J. Physiology 233(1978) 171.
- F. E. Yates, Amer. J. Physiology 238(1980)277.
- 0. E. Roessler, “Recursive evolution”, Biosystem l3(1979)193.
- T. Ikegami and K. Kaneko, to appear in Physica D(1992).
- I. Tsuda, “A hermeneutic process of the brain”, Prog. Theor. Phys. Suppl. 79 (1984) 241
- J. S . Nicolis and I. Tsuda, “Chaotic dynamics of information processing : The magic number seven plus-minus two revisited, Bull. of Math. Biol. 47(1985)343.
- 津田一郎、“脳の解釈学”(清水博編著「解釈の冒険」、NTT出版、1987)
- 津田一郎、「カオス的脳観」(サイエンス社、1990)
- 津田一郎、“神経回路におけるカオス力学系”(松岡清利編著 「ニューロコンピューティング-基礎と応用」、朝倉書店、1992

コメント