published in Physica A 392 (2013) 6084–6089
Yutaka Tachimori a,*, Hiroaki Iwanaga b & Takashi Tahara b
a Department of Social Welfare, Nihon Fukushi University, Chita-gun, Aichi, 470-3295, Japan
b Institute for basic Medical and Welfare research, Chuou-ku, Fukuoka, 810-0051, Japan
Abstract
Here, we constructed and analyzed a network (henceforth, “medical knowledge network”) derived from a commonly used medical text. We show that this medical knowledge network has small-world, scale-free, and hierarchical features. We then constructed a network from data from a hospital information system that reflected actual clinical practice and found that this network also had small-world, scale-free, and hierarchical features. Moreover, we found that both the diagnosis frequency distribution of the hospital network and the diagnosis degree distribution of the medical knowledge network obeyed a similar power law. These findings suggest that the structure of clinical practice may emerge from the mutual influence of medical knowledge and clinical practice, and that the analysis of a medical knowledge network may facilitate the investigation of the characteristics of medical practice.
Keywords: small- world; scale-free; complex network; natural language; medical knowledge
1. Introduction
Medical knowledge is extremely complicated. The number of diagnoses alone amount to tens of thousands. Other than diagnoses, an enormous quantity of knowledge is involved such as symptoms, results of clinical tests, pathological knowledge and anatomical knowledge. However, clinicians must make appropriate diagnoses on the basis of such complicated knowledge. How does the clinician select the appropriate diagnosis? One hypothesis is that the structure of medical knowledge itself helps a clinician diagnose. One approach to understanding the structure of medical knowledge is to classify that knowledge by using some predefined criteria, such as the International Classification of Diseases (ICD) [1]. If the purpose of using the classification is appropriate for the criteria, this approach is very useful. However, the criteria do not always fit actual clinical practice.
Complex networks have been studied extensively to determine the structures of many real systems, such as the World-Wide-Web (WWW), the Internet, and biological and social networks. These complex networks are frequently small-world and scale-free [2-6]. Small-world networks have a large clustering coefficient and a small average path length. Scale-free networks are characterized by a power-law decay of the degree distribution p(k)~k–α. Hierarchical organization of these complex networks has also recently been investigated [7, 8].
Medical knowledge is commonly described by natural language. Unlike classification by criteria, many properties of diseases are freely described. In description by natural language, various components of this medical knowledge are mutually connected in context, and a network is produced. This network may, in turn, influence clinical practice. However, the structure of this network and its influence on clinical practice is virtually unknown. Recently, a complex network analysis was applied to natural language [9, 10]. This analysis found that the language network has small-world and scale-free properties [11, 12]. Here, we applied this natural language analysis to medical knowledge and found similarities between the structure of the medical knowledge and that of clinical practice.
2. Methods
2.1 Construction of the medical knowledge network (MKN)
We analyzed “Harrison’s Principles of Internal Medicine, 15th Edition,” which is the major textbook on internal medicine. We analyzed only three chapters, “Disorders of the Cardiovascular System”, “Disorders of the Respiratory System,” and “Neurologic Disorders”, because the entire text was too large to analyze by hand. A total of 38353 sentences were comprised in these chapters, all of which were analyzed. Because the purpose of our analysis was to determine the structure of medical knowledge rather than language, we confined the subjects of study to only medical terms consisting of several words related to medical knowledge. We then classified these terms into four categories: “diagnosis”, “subjective symptom”, “objective symptom”, and “other medical terms”. For instance, “stomach cancer” is a term consisting of two words and classified as a “diagnosis”. This classification was made by two medical doctors and a healthcare information technologist. However, in this study, we used only the difference between “diagnosis” and the other three categories. All categories but “diagnosis” are prepared for future analyses. We then constructed the medical knowledge network as follows. First, we defined the medical terms as nodes of the network. Then, we defined edges that mutually connected a pair of terms in a sentence.
2.2 Construction of the diagnosis database network (DDN)
We also applied the network analyses to a database of “disease” in the hospital information system of Toyonaka Municipal Hospital. This database consisted of 218063 records, which were the data for 2 years. Each database record contained several items in addition to “diagnosis”, such as “patient ID”, “department code”, and “doctor ID”. Therefore, by assigning these items to nodes and mutually connecting all nodes in each record by edges, we constructed the diagnosis database network (DDN). This network is too large to analyze, so we analyzed a partial network consisting of randomly selected nodes as necessary.
Our use of these data was approved by Toyonaka Municipal Hospital. All of the patient data were de-identified, and because the analysis was purely statistical there were no ethics issues.
2.3 Network analysis
Network terms are defined as follows: the node is a fundamental unit of a network; the edge is a line connecting two nodes; the degree of a node is the number of edges connected to it (i.e. the number of neighbors); and the average path length is defined as the average minimal distance between any pair of nodes. Although the clustering coefficient has several definitions [13], we used the definition proposed by Watts and Strogatz [3]: The local clustering coefficient Cv for a single node v is defined as ,
where kv is the degree of the node. It is the probability that two nodes that are neighbors of a given node are also neighbors. The average clustering coefficient is defined as the mean of the local clustering coefficient for each node: \(C=\frac{1}{n}\sum_{\nu} C_\nu\) , where n is the number of nodes in the network. The corresponding random network is a random network with the same number of nodes and edges as the original network. The degree distribution p(k) is defined as the probability of a node having a degree of k . Scale-free networks are characterized by a power-law decay of the degree distribution p(k)~k–α. The exponent α is calculated from data using the method of maximum likelihood [14, 15].
3. Results
We constructed a network derived from a commonly used medical text (see Method). We henceforth call this network the medical knowledge network (MKN). We calculated the average path length and the average clustering coefficient of the MKN (see definitions in Method). The average path length was 4.317 and the average clustering coefficient was 0.86, the indication being that the MKN had nearly the same average path length and a far larger average clustering coefficient compared with the corresponding random network. These findings suggest that the MKN has the small-world property (Table 1). This small-world property may be necessary for a clinician to quickly find the correct diagnosis among a large number of diseases. In a small-world network, every node (i.e. every diagnosis) can be reached with only a few steps [9, 16].
| network | nodes | edges | C | Crandom | d | drandom |
|---|---|---|---|---|---|---|
| MKN | 47769 | 884613 | 0.86 | 7.75×10-4 | 4.317 | 3.07 |
| DDN | 44997 | 505565 | 0.83 | 4.99×10-4 | 3.894 | 3.44 |
Table 1 Profiles of the medical knowledge network (MKN) and the diagnosis database network (DDN). C: Average clustering coefficient, Crandom: Average clustering coefficient of the corresponding random network, d: Average path length, drandom: Average path length of the corresponding random network. For both the MKN and the DDN, the average path lengths are close to those expected for random graphs and C≫Crandom, meaning that both the MKN and the DDN have small-world features. For the DDN, we constructed a partial network by randomly selecting about 45000 nodes from the DDN and analyzed this partial network.
We also found that the degree distribution of the MKN exhibited a power law with a fast decaying tail (Fig.1a) [7, 17, 18]. This finding indicates that the MKN is a truncated scale-free network. The exponent was 2.045, which is consistent with many other complex networks whose exponents range from 2 to 3 [3, 13]. Scale-free behavior is a consequence of two generating mechanisms: networks expand continuously by the addition of new nodes, and new nodes attach preferentially to already well-connected sites (preferential attachment) [3, 19]. If the preferential attachment is completely fulfilled, the network exhibits the entire scale-free behavior; however, if the preferential attachment is not completely fulfilled because of, for example, limitations on available information, the scale-free behavior is truncated [15, 20-22]. For the MKN, our results suggest that the preferential attachment may be somewhat restricted.
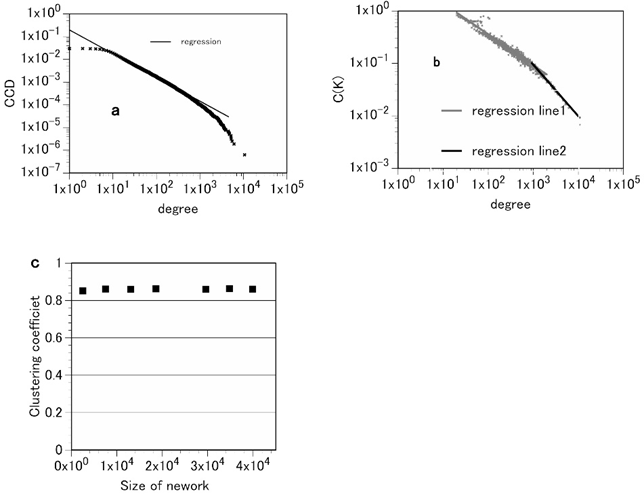
Figure 1. Attributes of the medical knowledge network (MKN). a, the complementary cumulative distribution of degrees for the MKN. The complementary cumulative distribution is defined as \( CCD(k)=\sum_{k\le j} p(j) \) , where p(j) is the probability of a node having a degree j (i.e., the degree distribution). This plot suggests that the degree distribution of the MKN is consistent with truncated power-law decay. The exponent of the degree distribution is 2.045. This figure indicates that this degree distribution follows a truncated power law (scale-free). A truncated scale-free distribution is a distribution that decays according to the power law p(k)~k–α followed by a sharp cutoff. b, the average of the clustering coefficients of nodes with k edges:C(k). C(k) follows the power law C(k)~k–ν where ν = 0.59 for small k and ν = 0.98 for large k. That is, at least for large k, the clustering coefficient follows the scaling law C(k)~k-1. c, the average clustering coefficient C is independent of the size of the network. By constructing partial networks by randomly eliminating several nodes from the MKN, we calculated the average clustering coefficients of the networks. This figure shows that the average clustering coefficients of the MKN are independent of the network size. These data demonstrate that the MKN has both properties of a hierarchical network.
We also investigated the hierarchical structure of the MKN. The preferential attachment model is a simple network growth model with no hierarchical structure [3]. In contrast, many networks in nature and society have some form of hierarchical structure. Recently, a network model that produces a network with a hierarchical structure was proposed [4, 6, 8]. According to this model, a network having a hierarchical structure has the following two features: the average clustering coefficient is independent of the size of the network, and the average of the clustering coefficients of nodes with k edges follows the scaling law C(k)~k-1. Our analysis of the MKN revealed that it has these two features (Fig. 1b, c).
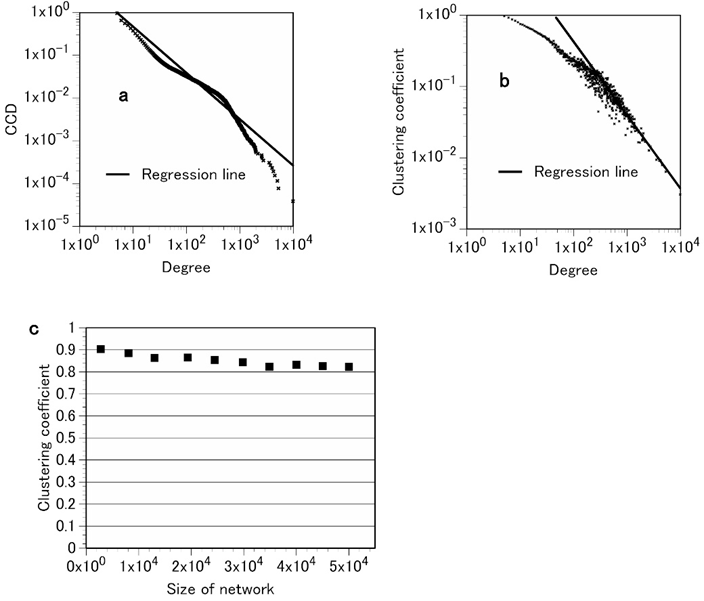
Figure 2. Attributes of the diagnosis database network (DDN) of Toyonaka Municipal Hospital. a, the complementary cumulative degree distribution of the DDN. These data show that the DDN degree distribution follows a truncated power law; the exponent is 2.084, which is similar to that of the MKN. b, the clustering coefficient of a node with degree k:C(k). As with the MKN, C(k) of the DDN follows the scaling law C(k)~k–ν where ν = 1.03 for large k. c, the average clustering coefficient C is independent of the size of the network. The average clustering coefficient of the DDN is independent of the system size. These data indicate that the DDN has both properties of a hierarchical network, similar to the MKN.
We next considered whether clinical practice also has small-world and scale-free properties. If the structure of the MKN reflects only that of the language itself, its application to real medical services would be restricted. However, if its structure affects the clinical behavior of medical professionals, its meaning would be significant. To answer this question, we applied the network analyses to a database of “disease” in a hospital information system, the database of which should reflect the clinical behavior of the doctors. This database comprised clinical diagnoses that the doctors had entered during daily medical examinations. We constructed a network derived from this database (see Method). We henceforth call this network the diagnosis database network(DDN).
Table 1 shows that the DDN has the small-world property. Figure 2 shows that the DDN is a truncated scale-free and hierarchical network. Furthermore, the average clustering coefficient and the power-law exponent of the DDN were 0.83 and 2.084, respectively, which are values similar to those of the MKN. Thus, both the DDN and the MKN have similar network structures.
As a final analysis of this study, we asked whether the degree distribution of diagnoses (diagnosis degree distribution) of the MKN obeys a power law similar to the frequency distribution of clinical diagnoses (diagnosis frequency distribution). We extracted the nodes classified as “diagnosis” from the MKN, and analyzed their degree distribution. We also analyzed the frequency distribution of internal medicine diagnoses from the hospital data. Both the diagnosis degree distribution of the MKN and the diagnosis frequency distribution of internal medicine followed truncated power laws with similar exponents of 2.10 and 1.84, respectively (Figure 3). In fact, the diagnosis frequencies of not only internal medicine but also other departments followed truncated power laws with exponents ranging from 1.76 to 2.20 [23, 24]. These findings may have important implications. In the knowledge network, a node is a term. Consequently, a term with a large degree is connected to many other terms, the result being that it frequently appears in many sentences. In fact, according to an investigation of a general text, the frequency of word appearance in a text and the degree of the network constructed from that text are positively correlated [25]. However, in this study the frequency is not the frequency of diagnosis appearance in the text but that of diagnosis appearance in the hospital. This distinction between our study and the preceding investigation may be important.
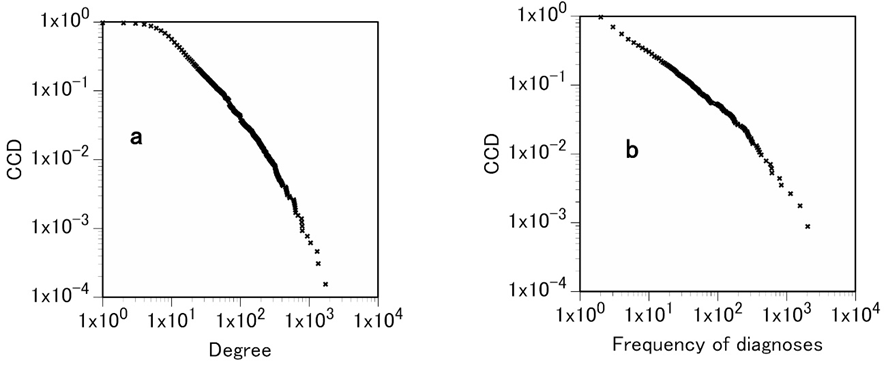
Figure 3. Degree and frequency of diagnosis. a, complementary cumulative diagnosis degree distribution of the partial network of the MKN consisting of only those nodes that were classified as “diagnosis” and their edges. This plot indicates that the diagnosis degree distribution follows a power law with an exponent of 2.10. b, complementary cumulative diagnosis frequency distribution of internal medicine of Toyonaka Municipal Hospital. The diagnosis frequency distribution follows a power law with an exponent of 1.84.
4. Discussion
As described above, the MKN displays small-world, scale-free, and hierarchical properties. The small-world property may help a clinician make the most appropriate diagnosis. In contrast, scale-free and hierarchical properties are related to the generating mechanism [3, 8]. Medical knowledge is always changing. This is the adaptation of medicine to change or progress in social situations and medical science. New medical terms, such as new diagnoses, are constantly being added to medical knowledge, and definitions of diagnoses frequently vary. The addition of a new term corresponds to the addition of a new node in the MKN. This new node is attached to already existing nodes. In this example, the possibility of attachment to frequently used terms (nodes) is thought to be large. This means that preferential attachment is applied to the MKN. Medical knowledge intrinsically involves a complex hierarchical structure. Therefore, new nodes need to be added to the MKN without damaging the preexisting hierarchical structure. Thus, the MKN would develop and evolve under the following two principles: preferential attachment and preservation of the preexisting hierarchical structure. These two principles may give the MKN its precise structure. These results suggest that the network analysis of medical texts may provide new insights into the genesis of medical knowledge.
We show that the diagnosis degree distribution of the MKN obeys a power law similar to the diagnosis frequency distribution of the hospital data. Why do these two distributions resemble each other? The answer to this question may be that medical texts continuously reflect new knowledge in clinical practice. Therefore, a disease that occurs frequently in clinical practice is likely to be described many times in the text. Similarly, a disease that is mentioned frequently in the text is easy for a doctor to recall in clinical practice. The doctor obtains medical knowledge from texts or medical articles; therefore, the knowledge in the doctor’s head would have a network structure similar to that of the texts. This mutual influence of medical knowledge and clinical practice may control the similar structures and distributions. That is, the similar structures may emerge from this mutual influence.
It used to be thought that diagnosis frequency was an objective index existing in the world; however, given the similarity between the diagnosis frequency of the hospital and the diagnosis degree of the MKN, diagnosis frequency could be influenced by medical knowledge. Medical knowledge influences clinical practice, and this practice influences the frequency of diagnosis. Because doctors diagnose through clinical practice, clinical practice is thought to be the observation of disease. Therefore, the fact that clinical practice influences diagnosis frequency implies that diagnosis frequency is not an objective index but, to a certain degree, a subjective index, the value of which varies somewhat with the observation of disease.
Finally, further network studies of medical knowledge and hospital data are needed, as are more detailed analyses (e.g., community structure [26, 27]) to clarify the features of clinical practice. Knowing how the structure of medical knowledge changes temporally may help us to clarify the features of medical adaptation to disease.
Acknowledgments
We would like to express our special thanks to Professor Ichiro Tsuda of Hokkaido University and Professor Takashi Yanagawa of Kurume University for continued encouragement and valuable comments. We also thank Toyonaka Municipal Hospital for providing data of the hospital.
Competing financial interests
The authors declare no competing financial interests.
References
[1] WHO, ICD-10: The ICD-10 Classification of Mental and Behavioural Disorders: Clinical Descriptions and Diagnostic Guidelines, World Health Organization, 1992.
[2] D. J. Watts, S. H. Strogatz, Collective dynamics of ‘small-world’ networks, Nature 393(1998) 440-442.
[3] A.-L. Barabási, R. Albert, Emergence of scaling in random networks, Science 286(1999)509-512.
[4] A.-L. Barabási, E. Ravasz, T. Vicsek, Deterministic scale-free networks, Physica A 299 (2001) 559–564.
[5] S. N. Dorogovtsev, A. V. Goltsev, J. F. Mendes, Pseudofractal scale-free web, Phys. Rev. E 65 (2002)066122.
[6] H. Jeong, B. Tombor, R. Albert, Z. N. Oltvai, A.-L. Barabási, The large-scale organization of metabolic networks, Nature 407 (2000) 651-654.
[7] E. Ravasz, A. L. Somera, D. A. Mongru, Z. N. Oltvai, A.-L. Barabási, Hierarchical organization of modularity in metabolic networks, Science 297 (2002) 1551-1555.
[8] E. Ravasz, A.-L. Barabási, Hierarchical organization in complex networks, Phys. Rev. E 67 (2003) 026112.
[9] R. F. Cancho, R. V. Solé, The small-world of human language, Proc. R. Soc. Lond. B 268 (2001) 2261-2266.
[10] R. V. Solé, B. C. Murtra, S. Valverde, L. Steels, Language networks: their structure, function and evolution, Complexity 15 (2010) 20-26.
[11] R. Solé, Syntax for free?, Nature 434 (2005) 289.
[12] A. E. Motter, A. P. S. de Moura, Y. -C. Lai, P. Dasgupta, Topology of the conceptual network of language, Phys. Rev. E 65 (2002) 065102(R).
[13] M. E. J. Newman, Networks An Introduction, Oxford University Press, Oxford NewYork, 2010.
[14] M. E. J. Newman, Power laws, Pareto distributions and Zipf’s law, Contemporary Physics 46 (2005) 323-351.
[15] A. Clauset, C. R. Shalizi, M. E. J. Newman, Power-law distributions in empirical data, SIAM Rev. 51 (2009) 661-703.
[16] M. Markošová, Network model of human language, Physica A 387 (2008) 661-666.
[17] R. F. Cancho, R. V. Solé, Least effort and the origins of scaling in human language, PNAS 100 (2003) 788-791.
[18] L. A. N. Amaral, A. Scala, M. Barthélémy, H. E. Stanley, Classes of small- world networks, PNAS 97 (2000) 11149-11152.
[19] R. Albert, H. Jeong, A.-L. Barabási, Error and attack tolerance of complex networks, Nature 406 (2000) 378-382.
[20] S. Mossa, M. Barthélémy, H. E. Stanley, L. A. N. Amaral, Truncation of power law behavior in “scale-free” network models due to information filtering, Pys. Rev. Lett. 88 (2002) 138701.
[21] S. N. Dorogovtsev, J. F. F. Mendes, Evolution of reference networks with aging, Phys. Rev. E 62 (2000) 1842.
[22] T. Maschberger, P. Kroupa, Estimators for the exponent and upper limit, and goodness-of-fit tests for (truncated) power-law distributions, Mon. Not. R. Astron. Soc. 395 (2009) 931-942.
[23] Y. Tachimori, T. Tahara, Clinical diagnoses following Zipf’s law, Fractals 10 (2002) 341-351.
[24] W. Fink, V. Lipatov, M. Konitzer, Diagnoses by general practitioners: Accuracy and reliability, Int. J. Forecasting 25 (2009) 784-793.
[25] R. F. Cancho, R. V. Solé, R. Köhler, Patterns in syntactic dependency networks, Phys. Rev. E 69 (2004) 051915.
[26] M. Girvan, M. E. J. Newman, Community structure in social and biological networks, PNAS 99 (2002) 7821-7826.
[27] M. E. J. Newman, Fast algorithm for detecting community structure in networks, Pys. Rev. E 69 (2004) 066133.

コメント