Y. Tachimori , H. Iwanaga , T. Tahara
Published in Physica A 392 (2013) 6084–6089
注は英語論文には無い。理解しやすいように追加した。
要約
省略
1. はじめに
医療知識は非常に複雑である。病名だけでも数万個を数える。病名以外にも、症状、検査結果、病理的知識、解剖的知識など膨大な量の知識を扱っている。医師はこのような大量、複雑な知識を扱いながら患者に対して適切な診断を行わねばならない。医師はこのように多数の病名の中から如何にして適切な診断ができるのであろうか。一つの仮説として、医師が扱う医療知識そのものに診断を支えるための構造が含まれているという考えがある。医療知識を分類する試みは従来から多くおこなわれている。例えばICD-10は古くからおこなわれている病名分類である [1]。ただ、ICD-10 を含めて今までのすべての分類は何らかの基準(臓器別、病理別、原因別)を決めてそれによる分類である。このような分類はある基準に沿っての利用においては大いに役にたつ。しかし、個々の診療業務は必ずしもそのような分類基準に沿って行われるわけでない。ある病名を決定する道筋は多様である。
近年、World-Wide-Web (WWW)、細胞の代謝、社会ネットワークなど複雑(complex)な構造を表すために複雑系ネットワーク(complex networks)の理論が進歩してきている。それらの複雑な構造物に共通にみられる一般的な性質(generic properties)としてスモールワールド性とスケールフリー性がある[2-6]。スモールワールド性とは大きなクラスター係数と小さな平均距離を特徴とする。スケールフリー性とは各nodeの次数分布がべき法則(P(k)∝k-α)に従うという性質である。さらに最近、これら以外の性質として階層構造も論じられている[7,8]。
医療知識はすでに述べたような一つの軸による分類以外に自然言語によって記述される場合が多い。その場合は決まった基準による分類とは異なり、病気の多様な性質、多様な症状、多様な原因が他の病気との関連の中で自由に記述される。そのような自然言語による病気の記述は一つの基準に基づく分類に比べて複雑な知識構造を記述する場合に優れている。しかし、このような自然言語による記述は逆にその記述の自由さによって知識全体の構造を把握するのを難しくしている。 近年、複雑系ネットワーク分析が自然言語に適用されている[9, 10]。この分析によって前述のスモールワールド性やスケールフリー性が言語の中にも出現することが分かっている[11, 12]。本講では医学教科書の記述に対して自然言語分析の方法を使い、医学知識がスモールワールド性やスケールフリー性、階層性を持っていることを示す。さらに、実際の病院のオーダリングデータが同じ性質を持つことを示し、医療知識の構造が実際の医療行動に対しても影響を与えていることを示す。さらに、実際の病院のオーダリングデータが同じ性質を持つことを示し、医療知識の構造が実際の医療行動に対しても影響を与えていることを示す。
2. 方法
2.1 医療知識ネットワーク(medical knowledge network:MKN)の構築
医学知識の記述の代表として内科学の標準的教科書であるハリソンの「内科学」(日本語翻訳版)を採用した。ただ、作業の都合上、そのテキスト内から「循環」、「呼吸」、「神経」の3つの章のみを分析した。本来は膨大なテキストであるがこの3つの章で38353行の文が含まれている。我々の目的は、言語よりむしろ医療知識の構造を明らかにすることであるので、医療知識と関係する医学用語のみを対象とした。これらの医学用語(medical term)を診断名(d)、自覚症状(s)、他覚的異常(f)、その他の医学用語(x)に分類した。例えば、病名を表すstomach cancerは二つの単語から成る診断名に分類されるtermである。このような分類作業は二人の医師と一人の医療情報技師によって成された。文章にはtermに含まれない冠詞、接続詞、動詞、副詞、形容詞なども含んでいるが、これらの単語は今回の分析の対象からは外した。また、今回の研究では、診断名とそれ以外の医学用語との違いのみを検討した。診断名以外の用語については今後の研究課題とした。一つの文に含まれる各term(node)をネットワークのnodeとした。そして、一つの文内のnode同士を互いにedgeにて連結(connect)した。
2.2 病名データベースネットワーク(diagnosis database network:DDN)の構築
我々はネットワーク分析を市立豊中病院の病院情報システム内の病名データベースにも適用した。このデータベースには218063レコードが含まれている。これは、この病院の2年間分のデータである。このデータベースの一つのレコードは診断名以外に、患者ID、診療科コード、医師IDが含まれている。そこで、これらの4つの項目をnodeとし、一つのレコードに含まれるnodeを互いにedgeにて連結することにより病名データベースネットワーク(diagnosis database network:DDN)を構築する。このネットワークは分析するには大きすぎたので、このネットワークからランダムに選んだnodeからなる部分ネットワークを分析した。 これらのデータは市立豊中病院から提供を受けた。その際、全ての患者の個人情報は削除し、全ての分析は純粋に統計分析のみとし倫理問題を無くした。
2.3 ネットワーク分析
ネットワーク分析に使う用語は次のように定義される。
node:ネットワークの基本要素
edge:二つのnodesを繋ぐ線
nodeの次数(dgree):そのnodeに繋がったedgeの数(言いかえると、近傍の数)
平均経路長(average path length):任意の二つのnodesを繋ぐ最小距離の平均
クラスター係数:多くの定義[13]があるが、ここではWattsとStrogatzの定義[3]を採用する。あるnodeνの局所クラスタ係数Cνを次のように定義する。
ここで、kνはnode νの次数
これは、あるnodeの任意の二つのnodesが再び互いに近傍である確率である。平均クラスタ係数は局所クラスタ係数の平均と定義される: \(C=\frac{1}{n}\sum_{\nu} C_\nu\) ここで、nはこのネットワークのnodesの数である。
対応ランダムネットワーク:考えているネットワークと同じ数のnodeとedgesをもつランダムネットワークのことである。
次数分布p(k):次数kをもつnodeの確率と定義する。
スケールフリーネットワーク(Scale-free networks):次数分布がべき法則で減衰するネットワークと定義する。すなわち、 。この指数αはデータからmaximum likelihood法で計算される[14, 15]。
3. 結果
方法のところで述べたように、普通に使われる医学教科書からネットワークを構築した。このネットワークを以後medical knowledge network (MKN)と呼ぶことにする。このMKNの平均経路長(average path length)と平均クラスター係数(average clustering coefficient)を計算した。平均経路長は4.317であり、平均クラスター係数は0.86であった。これは、MKNが対応するランダムネットワークに比べるとほぼ同じ平均経路長をもち、ずっと大きな平均クラスター係数を持っていることを示している(注:MKNと同じnode数とedge数をもつ対応するランダムグラフの平均距離は3.07でありクラスター係数は0.0008である)。これは、すなわちMKNがスモールワールドの性質を持っていることを示している(Tabel1)。このようなスモールワールドの性質は、臨床医に非常に多数の病気から素早く正しい診断を行うために必要なのかもしれない。スモールワールドネットワークにおいては全てのnode(すなわち、全ての診断)はわずかのstepで到達できる[9, 16]。
注:医師が診療を行うときには膨大な知識から適切な病名を選び出す。患者が示す症状や検査成績から数万個に及ぶ病名の中から素早く適切な病名と選んでいる。医療知識がスモールワールドの構造を持っていることは症状や検査成績からわずか5ステップ以内に適切な病名にたどり着くことができることを示している。医療知識がスモールワールド性を持つことはこのような連想を行う際に非常に有効であると考えられる。
| network | nodes | edges | C | Crandom | d | drandom |
|---|---|---|---|---|---|---|
| MKN | 47769 | 884613 | 0.86 | 7.75×10-4 | 4.317 | 3.07 |
| DDN | 44997 | 505565 | 0.83 | 4.99×10-4 | 3.894 | 3.44 |
Table 1
Profiles of the medical knowledge network (MKN) and the diagnosis database network (DDN). C: Average clustering coefficient, Crandom: Average clustering coefficient of the corresponding random network, d: Average path length, drandom: Average path length of the corresponding random network. For both the MKN and the DDN, the average path lengths are close to those expected for random graphs and C≫Crandom, meaning that both the MKN and the DDN have small-world features. For the DDN, we constructed a partial network by randomly selecting about 45000 nodes from the DDN and analyzed this partial network.
Fig.1aに示すようにMKNのdegree distribution(次数分布)は非常に早く減衰するtailを持つ power-law distributionを示す[7, 17, 18]。すなわち、このネットワークは(truncated) scale-free networkである。その時のべき指数は2.045である。スケールフリー性は多くの複雑系ネットワークや言語のネットワークで見られている。その際の指数が2~3であるという結果は今回の結果と一致している[3, 13]。スケールフリー性は二つの生成メカニズムの結果である:ネットワークに新しいnodesが付け加わることにより連続的に成長することと、その際、新しいnodesはすでに多くの近傍をもつnodesに優先的に接続する(優先選択原理 preferential attachment)ことである[3, 19]。優先選択原理が完全に満たされる場合には「べき法則」が成り立つ。しかし、優先選択原理は実際のネットワークの生成では、使える情報の制限のため完全に満たされることは少ない。優先選択原理が、完全には満たされない場合には分布はtruncate される[15, 20-22]。MKNに関して、結果から見ると優先選択原理は何らかの制限を受けていると考えられる。
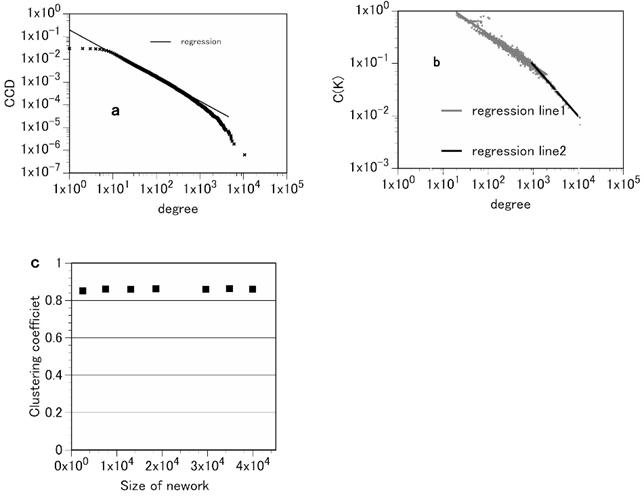
Figure 1. Attributes of the medical knowledge network (MKN). a, the complementary cumulative distribution of degrees for the MKN. The complementary cumulative distribution is defined as \( CCD(k)=\sum_{k\le j} p(j) \) , where p(j) is the probability of a node having a degree j (i.e. the degree distribution). This plot suggests that the degree distribution of the MKN is consistent with truncated power-law decay. The exponent of the degree distribution is 2.045. This figure indicates that this degree distribution follows a truncated power law (scale-free). A truncated scale-free distribution is a distribution that decays according to the power law p(k)~k–α followed by a sharp cutoff. b, the average of the clustering coefficients of nodes with k edges:C(k). C(k) follows the power law C(k)~k–ν where ν = 0.59 for small k and ν = 0.98 for large k. That is, at least for large k, the clustering coefficient follows the scaling law C(k)~k-1. c, the average clustering coefficient C is independent of the size of the network. By constructing partial networks by randomly eliminating several nodes from the MKN, we calculated the average clustering coefficients of the networks. This figure shows that the average clustering coefficients of the MKN are independent of the network size. These data demonstrate that the MKN has both properties of a hierarchical network.
MKNのより詳しい特徴を知るためにネットワークの階層構造についても調べた。優先選択モデル(BAモデル)は構造を持たない成長モデルである[3]。それに対して現実のネットワークはその内部に何らかの階層構造を持っている場合が多い。最近、階層構造を生み出すネットワークモデルが提案されている[4, 6, 8]。(注:ここで階層的組織化(hierarchical organization)とは小さなnodeのグループが階層的な方法で大きなグループに組織化されることを意味している。)モデルが述べるところによれば、ネットワークが階層的組織化によって生み出された場合には次の二つの性質を持っている。すなわち、①クラスター係数がネットワークの大きさによらない(independent)こと、②次数がkのnodeの平均クラスター係数C(k) が指数1のべき法則(power-law)を満たす( )という二つである。MKNの分析によれば、MKNはこれら二つの条件を満たしていることが確認された(Fig. 1b, c)。
注:以上の事実から、MKNはスモールワールドでスケールフリー性と階層構造をもつネットワークであることが示された。スモールワールド性の医療における意味は前述したとおりであり、医師による診断を可能とさせるために重要である。一方、スケールフリー性と階層構造はその医療知識の生成メカニズムと関係していると考えられる。医療の知識は常に変化している。病名の追加、定義の変化、新しい知識の追加、古い知識の削除などが行われる。新しい知識はMKNにおける新しいnodeの追加に対応する。新しく追加されたnodeはすでにあるnodeとlinkされる。その際、よりたくさん使われる知識とlinkされる可能性が高まることは十分考えられる。これはその接続において優先選択原理が働くことを意味している。また、医学の知識は複雑な階層構造を持っている。新しくnodeを追加する場合に旧来の階層構造を保ちながら成長する必要がある。このような二つの原理が働いて医療知識が成長していくものと考えられる。今回行ったようなテキストを利用した医療知識ネットワークの分析は医療の知識の成り立ちに対して新しい知見を与える可能性がある。
次に我々は医療知識のみならず医療行動自体にスモールワールド性とスケールフリー性が見られるかどうかを調べた。医療知識ネットワークが医療テキストという文章が示す構造のみを示しているならば、(医療知識ネットワークの)実際の医療における利用、応用は限られる。しかし、もし、このネットワーク構造が医療者の医療行動に影響するならばその意味することは重大である。我々は医師の行動を反映しているデータとして、病院情報システム内の病名データベースのデータを利用した。病名データベースは医師の日常の診療において、診察している患者の病名をその都度、コンピュータに入力することにより作られたデータベースである。このデータベースから方法において述べたようにネットワークを構築した。これ以後、このネットワークをdiagnosis database network(DDN)と呼ぶ。注:データベース内の病名は必ずしも確定診断を意味するものではなく、仮の病名である。患者の仮の病名は診療や検査を行うにしたがって変化する場合もある。そのような場合には同じ患者について何種類もの病名が登録されていく。すなわち、患者に対する診療行動に従って登録される病名は変化していくのである。
Table1はDDNがスモールワールドの性質を持つことを示している。さらに、Fig.2a,b,cに示すようにDDNの次数分布はtruncated power lawに従い、MKNと同様にスケールフリーで階層構造を持つネットワークであることが示された。しかも、DDNの平均クラスター係数は0.83、べき指数は2.084であり、MKNのそれらはそれぞれ0.86と2.045といずれも非常に近い値である。これらの事実はDDNがMKNと非常に似たネットワーク構造を持っていることを示している。注: 医師の病名付けという行為のネットワークを表しているDDNとテキストから作られた医療知識ネットワークが非常に似通った性質を持っていることは驚くべき事実である。
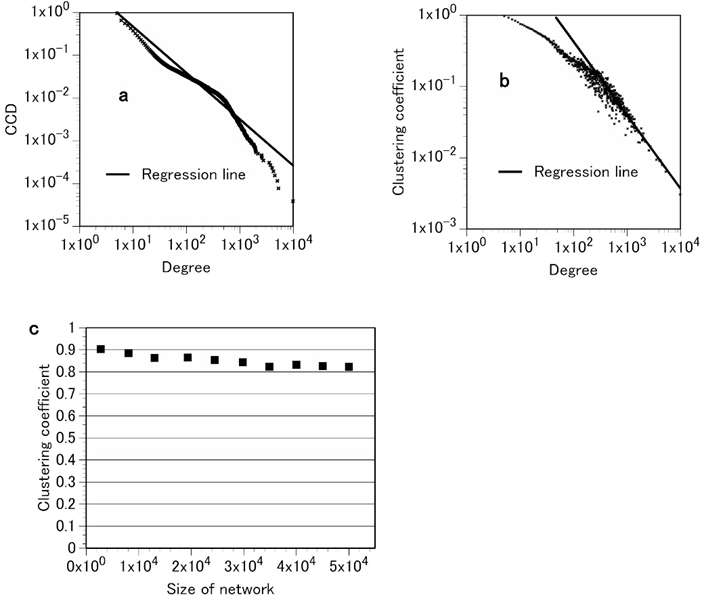
Figure 2. Attributes of the diagnosis database network (DDN) of Toyonaka Municipal Hospital. a, the complementary cumulative degree distribution of the DDN. These data show that the DDN degree distribution follows a truncated power law; the exponent is 2.084, which is similar to that of the MKN. b, the clustering coefficient of a node with degree k: C(k). As with the MKN, C(k) of the DDN follows the scaling law C(k)~k–ν where ν = 1.03 for large k. c, the average clustering coefficient C is independent of the size of the network. The average clustering coefficient of the DDN is independent of the system size. These data indicate that the DDN has both properties of a hierarchical network, similar to the MKN.
最後に我々は実際の病名頻度の分布と知識ネットワークにおける診断名termの次数分布の関係を調べた。Fig.3aはMKNから診断名と分類されているnodeをのみを取り出してその次数分布(診断名次数分布)を調べた。さらに、病院データベースから内科における病名の頻度分布を調べた。MKNからの診断名次数分布も内科の病名頻度分布もどちらもtruncated power lawを示し、そのべき指数はそれぞれ、2.10と1.84であり似た値を示した(Figure 2)。内科における病名頻度だけでなく、他の診療科の病名頻度もやはりtruncated power lawを示し、その指数は1.76から2.20の範囲に入っている[23, 24]。実際の病名頻度とMKNの診断名次数分布が同じように「べき法則」に従うことは非常に示唆的である。知識ネットワークにおけるnodeとはtermである。それで、termが大きな次数をもつということは、そのtermが多くの他のtermとつながっていることを示している。このことは、そのtermが文章の中に高頻度で出現することを示している。実際、一般的な文章の分析によれば、文章中のある語の出現頻度とその文章により構築されるネットワークにおける次数には正の相関がみられる[25]。しかし、文章の場合はその文章内の単語の頻度である。しかし、今回の結果は文章内の病名の出現頻度ではなく、実際の診療における病名頻度と次数が相関することを示している。このことの意味するところは少し異なっているし、より重要な結果であると考えられる。
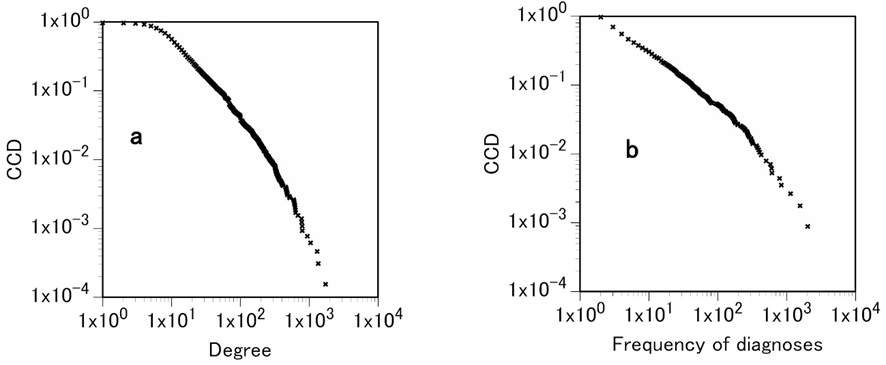
Figure 3. Degree and frequency of diagnosis. a, complementary cumulative diagnosis degree distribution of the partial network of the MKN consisting of only those nodes that were classified as “diagnosis” and their edges. This plot indicates that the diagnosis degree distribution follows a power law with an exponent of 2.10. b, complementary cumulative diagnosis frequency distribution of internal medicine of Toyonaka Municipal Hospital. The diagnosis frequency distribution follows a power law with an exponent of 1.84.
4. 考察
上で示したように、MKNはスモールワールド、スケールフリー、階層構造を示す。スモールワールドという性質は臨床医の診断行為を助けると思われる。反対に、スケールフリーと階層構造ははMKNの生成メカニズムに関係する[3, 8]。医療知識は常に変化している。これは社会環境や医学の変化や進歩に対する適応である。新しい診断名などの新しい医学用語は医療知識の中に常に加えられ、診断名の定義はしばしば変化する。新しい用語の追加はMKNにおける新しいnodeの追加に対応している。追加された新しいnodeは既に存在するnodeに連結される。その際、よく使われる用語(node)への接続の可能性はより多いと考えられる。これは、優先選択原理( preferential attachment)がMKNに適応されることを意味している。医療知識は本質的に複雑階層構造を持っている。それ故、新しいnodesの追加は元々ある階層構造を損なわないように行われる必要がある。このようにして、MKNは次の二つの原理、すなわち優性選択原理と既存の階層構造の維持に従って成長、発展するであろう。これら二つの原理がMKNの特徴的な構造を決めていると思われる。このような結果は、医療テキストに対するネットワーク分析が医療知識の生成に新しい見方を与えるかもしれない。
MKNにおける診断nodeの次数が病院の診断名の頻度と同様のベキ乗則に従うことを示した。何故この二つの分布が同じような性質を示すのであろうか。これは、医学テキストが臨床の新しい知見を反映し続けているためかもしれない。それ故、臨床の場で高頻度で起こる病気はテキストにおいても高頻度で記述される。同様に、テキストに高頻度で記述される病気は臨床においても想起されやすくなる。医師はテキストや医療文章から医学知識を得ている。そのため、医師の頭にある知識はテキストにあるのと同様のネットワーク構造を持つようになるであろう。このような医療知識と臨床行為の間の相互作用が似通った構造と分布を生み出しているのかもしれない。すなわち、似通った構造はこのような相互作用から生まれるのであろう。
従来、病名の頻度とは世の中に客観的に存在する指標であると考えられていた。しかし、病名頻度分布が医療知識ネットワークの次数分布と似ているということは病名頻度が医療知識の影響を受ける可能性があることを意味している。医療知識は医師の診療行動に影響を与えそれを通じて病名の頻度に影響を与える。医師はその診療行動によって患者を診断するのであるから、診療行動とは医師の病気に対する観測行為と考えることができる。病名の頻度が医師の行動に影響されるということは、病名頻度という指標が観測の影響を受けるということを意味している。従来、病名頻度は客観的な指標であると考えられていた。しかし、今回の結果は病名頻度が観測の影響によって値が変化しうる指標であるという新しい考え方を示唆しているのである。
最後に、医療知識や病院データに関してより多くのネットワーク研究が必要である。コミュニティ行動などのより詳細な分析により臨床行動の特徴を明らかに出来るであろう。医療知識の構造が土曜用に変化するかを知ることによって、病気に対する医療の適応の特徴を明らかにすることが出来るかもしれない。
Acknowledgments
北海道大学の津田一郎先生、久留米大学の柳川堯先生による適切なアドバイスに心から感謝します。また、豊中病院には病院データの提供を受けたことに感謝します。
Competing financial interests
本論文に関して,開示すべき利益相反関連事項はない。
References
[1] WHO, ICD-10: The ICD-10 Classification of Mental and Behavioural Disorders: Clinical Descriptions and Diagnostic Guidelines, World Health Organization, 1992.
[2] D. J. Watts, S. H. Strogatz, Collective dynamics of ‘small-world’ networks, Nature 393 (1998) 440-442.
[3] A.-L. Barabási, R. Albert, Emergence of scaling in random networks, Science 286(1999) 509-512.
[4] A.-L. Barabási, E. Ravasz, T. Vicsek, Deterministic scale-free networks, Physica A 299 (2001) 559–564.
[5] S. N. Dorogovtsev, A. V. Goltsev, J. F. Mendes, Pseudofractal scale-free web, Phys. Rev. E 65 (2002) 066122.
[6] H. Jeong, B. Tombor, R. Albert, Z. N. Oltvai, A.-L. Barabási, The large-scale organization of metabolic networks, Nature 407 (2000) 651-654.
[7] E. Ravasz, A. L. Somera, D. A. Mongru, Z. N. Oltvai, A.-L. Barabási, Hierarchical organization of modularity in metabolic networks, Science 297 (2002) 1551-1555.
[8] E. Ravasz, A.-L. Barabási, Hierarchical organization in complex networks, Phys. Rev. E 67 (2003) 026112.
[9] R. F. Cancho, R. V. Solé, The small-world of human language, Proc. R. Soc. Lond. B 268 (2001) 2261-2266.
[10] R. V. Solé, B. C. Murtra, S. Valverde, L. Steels, Language networks: their structure, function and evolution, Complexity 15 (2010) 20-26.
[11] R. Solé, Syntax for free?, Nature 434 (2005) 289.
[12] A. E. Motter, A. P. S. de Moura, Y. -C. Lai, P. Dasgupta, Topology of the conceptual network of language, Phys. Rev. E 65 (2002) 065102(R).
[13] M. E. J. Newman, Networks An Introduction, Oxford University Press, Oxford NewYork, 2010.
[14] M. E. J. Newman, Power laws, Pareto distributions and Zipf’s law, Contemporary Physics 46 (2005) 323-351.
[15] A. Clauset, C. R. Shalizi, M. E. J. Newman, Power-law distributions in empirical data, SIAM Rev. 51 (2009) 661-703.
[16] M. Markošová, Network model of human language, Physica A 387 (2008) 661-666.
[17] R. F. Cancho, R. V. Solé, Least effort and the origins of scaling in human language, PNAS 100 (2003) 788-791.
[18] L. A. N. Amaral, A. Scala, M. Barthélémy, H. E. Stanley, Classes of small- world networks, PNAS 97 (2000) 11149-11152.
[19] R. Albert, H. Jeong, A.-L. Barabási, Error and attack tolerance of complex networks, Nature 406 (2000) 378-382.
[20] S. Mossa, M. Barthélémy, H. E. Stanley, L. A. N. Amaral, Truncation of power law behavior in “scale-free” network models due to information filtering, Pys. Rev. Lett. 88 (2002) 138701.
[21] S. N. Dorogovtsev, J. F. F. Mendes, Evolution of reference networks with aging, Phys. Rev. E 62 (2000) 1842.
[22] T. Maschberger, P. Kroupa, Estimators for the exponent and upper limit, and goodness-of-fit tests for (truncated) power-law distributions, Mon. Not. R. Astron. Soc. 395 (2009) 931-942.
[23] Y. Tachimori, T. Tahara, Clinical diagnoses following Zipf’s law, Fractals 10 (2002) 341-351.
[24] W. Fink, V. Lipatov, M. Konitzer, Diagnoses by general practitioners: Accuracy and reliability, Int. J. Forecasting 25 (2009) 784-793.
[25] R. F. Cancho, R. V. Solé, R. Köhler, Patterns in syntactic dependency networks, Phys. Rev. E 69 (2004) 051915.
[26] M. Girvan, M. E. J. Newman, Community structure in social and biological networks, PNAS 99 (2002) 7821-7826.
[27] M. E. J. Newman, Fast algorithm for detecting community structure in networks, Pys. Rev. E 69 (2004) 066133.

コメント