日月 裕
「医療の不確実性」という言葉がある。医療経済の領域でも昔からいわれている言葉である。この不確実性は医療原価管理をはじめ、医療の管理において重大な影響を与える。
医療の現場にいれば、不確実性は日常的なことである。例えば、医療においては自分の領域(守備範囲)を完全に決めることが出来ない。医療以外の領域ではその企業や店の守備範囲がきっちり決まっている。マクドナルドはハンバーガーしか扱わない。客がハンバーガーを嫌いだと言っても、ハンバーガー以外を提供することはない。それに対して、医療においては、もし虫垂炎のみを扱いたいと医師が希望しても不可能である。虫垂炎だと思って手術しても卵巣軸捻転かもしれない、癌であるかも知れない、憩室炎かもしれない。脳外科の専門医だとしても間違って眼科の患者が来ることもある。専門領域のみを扱えばよいのならば、医師ももっと簡単に医療を行えるがそのようなわけにはいかない。
医師だけではない。医療において患者の範囲を限定できない状況はしばしばある。日本では救急医療は軽症患者の1次医療、入院が必要と認められる患者のための2次医療、高度な救命医療を行う3次医療に分かれている。しかし、3次医療機関に軽症の患者が受診することは日常茶飯事であり、1次医療機関に心筋梗塞の患者が受診することも稀ではない。これは、「患者が間違って受診するから」とは必ずしも言えない。もし、医療者が前もってトリアージ(triage、患者の重症度に基づいて治療の選別を行うこと)を行ったとしても間違いは必ず起こるであろう。もし、1次医療機関に軽症しか受診しなくて3次医療機関には生命危機の患者しか受診しないなら医療はもっと単純になるであろう。
病院の入院日数が問題になっている。しかし、これも日常臨床で経験することであるが、治療の期間を限定することは出来ない。1週間で治ると思って入院させた患者が3ヶ月かかることもあるのである。帝王切開で大量出血して死亡するという事故が時々起きる。不幸な事故である。輸血さえ間に合えば助かる命かもしれない。「手術の際の輸血準備量を決めることぐらいやさしい」と思われるかもしれない。そのように思って、昔から多くの病院で輸血準備量の決定を試みてきた。しかし、いまだに準備量を決定することが出来ない。もし、すべての手術に対して十分安全であると思われる血液準備をするならば、準備血の大半が使われないで廃棄されることになるであろう。
街中にあるコンビニエンスストアでも販売商品のデータベースを分析することで適正な在庫を決定している。しかし、医療では適正在庫をいまだに決定することが出来ない。何ヶ月も使わないので、必要ないと思って在庫からはずした次の日に必要になるということがしばしば起こる。医療は遅れているのであろうか。他の産業では出来ている仕事内容の限定、在庫の管理、適切な費用管理、これらが医療においてはあまりうまくいっていない。
以上のように、現場においては医療の不確実性は日常的なことである。従来、「科学は確実である」という信念が広くいきわたっていた。そのことから、医療の不確実性は、医療が科学ではないために起こるという考えも起こっている。しかし、「科学が確実である」という信念は20世紀半ばのカオス理論の進展によって崩れ去っている。本項では、医療における不確実性が、医療に内在する複雑系の性質に由来することを示したい。
※当記事は、『新たな病院原価計算を創る-複雑系との対話-』(田原孝編、田原孝・平井孝治・日月裕著, 講談社エディトリアル, 2022)の第Ⅲ部である。
第1章 線形、非線形、力学系、そしてカオス、複雑系へ
1.線形、非線形
1-1 要素還元主義
近代科学の哲学的基礎を作ったデカルトの要素還元主義とは次のようなものである。
1) 明晰で判明なもののみを真と認めること。
2) 問題はできるだけ多くの、そして細かな部分や要素に分割すること。
3) 全体を知るには、もっとも単純な部分や要素からはじめて、もっとも複雑なものの認識まで積み上げていくこと。
4) このとき細かく分割した部分や要素は1つでも取り落とすことなく、すべて取り上げて構成すること。
要点は二つである。一つは細かな要素に分解すること、二つ目は全体を知るためには分解した要素を積み上げることである。
この二番目の積み上げ方に線形と非線形の違いがある。積み上げるときに要素間に線形の関係がある(もしくは、関係が無いといっても良い)と考えて積み上げるのが線形理論であり、非線形の関係が有ると考える理論が、カオス理論や複雑系理論などの非線形理論である。どちらも、要素に分解するという点では変わりがない1 。分解することそのものを否定するホーリズム(全体論)とは考え方が異なっている。
1-2 線形性
線形関係とは、直感的には積み上げるときに各要素の性質が変化しないで全体にそのまま積みあがるという関係である。例えば質量は考えると全体の質量は各要素の質量を単純に積み上げた(足し算)ものである。数学的には線形関係(関数の)は 次のように表される。
\begin{equation}
f(x+y)=f(x)+f(y) \qquad f(cx)=cf(x)\tag{Ⅲ-1-1}
\end{equation}
これは関数 \(f(x)\) が線形であることの定義 2であるが、最初の例でいえば、次のように解釈される。ここで、\(f(x)\) がある要素 \(x\) の質量を表すとすると、最初の式は二つの要素をあわせた質量はそれぞれの質量の和であるということである。二番目の式はある要素 \(c\) 個の質量はその要素の質量の \(c\) 倍であるということを表している。数学ではこのように定義するが、もし、\(x\) や \(f(x)\) が普通の数であるならば、このような関係を満たす関数は
\begin{equation}
f(x)=ax\tag{Ⅲ-1-2}
\end{equation}
だけであることが証明されている( \(a\) は定数)。これは、よく知られた直線の式である。すなわち、変量 \(x\) と \(y\) が線形関係にあるとは、この二つの変量が直線関係にある ( \(y=ax\) という関係にある)ということである3。
二つの変量は何を表していてもよい。変量 \(x\) がばねの長さの変化量、\(y\) がばねの引く力であれば、この関係はバネのフックの法則である。時間的にある量が変化するときに、ある時刻の量と次の時刻の量の関係でも良い。例えば貯金を考える。ある月の貯金を \(x\)、次の月の貯金額を \(y\)、一月の利息を \(a\) とすると、
\begin{equation}
y= (1+a) x
\end{equation} となる。これも、線形関係である。
ここで、それぞれの月を \(n\) で表すと、ある月 \(n\) の預金額は \(x\) の替わりに \(x_n\) と表される。
さらに、\(y\) は \(x_{n+1}\) と表され、上記の関係は
\begin{equation}
x_{n+1}=(1+a)x_n\tag{Ⅲ-1-3}
\end{equation}
と表される。この式は最初の月(例えば貯金を始めた月)の預金額x0を決めれば、順番に計算することによりある月nの預金額xnをnの関数として求めることが出来る。すなわち
\begin{equation}
x_n=(1+a)^nx_0\tag{Ⅲ-1-4}
\end{equation}
となる。これは、預金額を月の関数として表した式である。式(Ⅲ-1-3)は貯金の変化を支配する関係であり、これは線形関係である。そして、得られた式(Ⅲ-1-4)は時間(月を単位としている)と貯金額の関係を表す式であるが、この式はいわゆる指数関数であり非線形関数である。
式(Ⅲ-1-3)は一つの変量の変化を見るための式であるが、複数の変量の変化を見る場合にも使える。例えば、二つの銀行AとB(利率はそれぞれ \(a\) , \(b\) とする)に貯金をしている(月 \(n\) でのそれぞれの預金額を \(x_n\) 、\(y_n\) とする)。さらに、Bの預金額の一定割合( \(c\) )を毎月Aに移しているとする。このときのA、B銀行の預金額の変化は次のように表される。
\centering
\begin{eqnarray}
\left\{
\begin{array}{l}
x_{n+1}=(1+a)x_n+cy_n \\
y_{n+1}=(1+b)(1-c)y_n\tag{Ⅲ-1-5}
\end{array}
\right.
\end{eqnarray}
この式によって、毎月の二つの銀行の預金の変化を求めることが出来る。これも時間変化を表す線形の関係である。このような場合は二つの変量\(x\)と\(y\)が線形に相互作用していると呼んでいる。
物理などでは運動や状態の変化を調べるのに(Ⅲ-1-3)あるいは(Ⅲ-1-5)4のような式で表す。物理では運動方程式や単に方程式などと呼んでいるが、ここでは変化を表す方程式という意味で「変化方程式」と呼んでおく。その変化方程式が線形であれば、(特に複数の変量の変化を表す場合は)線形相互作用と呼んでいる。
このように線形と言う言葉は大きく二つの意味に使っている。一つは関数の線形性、もう一つは変化方程式の線形性である。前にも述べたように線形相互作用をしている変量の時間変化は線形関数で表せないこともある5。
1-3 非線形性
非線形とは線形ではないという意味である。非線形関数、非線形相互作用、これらは線形でない関数、線形ではない相互作用という意味である。実は線形とは非常に特殊な関係である。世の中を見回したときに線形の関係や線形の相互作用はほとんどない。世の中は非線形だらけなのである。
一方人間が行っていることを見ると、そこには線形があふれている。人間が作るいろいろな機械、これらは多くの部品から成り立っているが、それらの部品どうしは線形の相互作用をしている(各部品が線形の動きをしているという意味ではない)場合が多い。機械を作るときには、まずある一つの働きをする部品を作る。そして、それらの部品を組み合わせて全体を作っている。そのさい、部品は全体に組みあがった後でも同じ働きをしている。例えば、ラジオの中身は複雑に見えるがそれらはいくつかの部品(部分)から成り立っている。電源を供給する部分、検波する部分、波形を増幅する部分、音を鳴らす部分などに分かれている。これらを組み合わせて一つのラジオにするのであるが、出来上がったラジオも電源を供給し、検波し、増幅をし、音を鳴らす機械でしかない。すなわち、各々の部分を足し算(線形性)した機能のみを全体が示すという意味で線形の機械である。
線形の分析は、社会現象を見たり分析したりする場合でも行われている。非線形の関数や相互作用を直接扱うのは非常に難しいので、多くの場合、線形近似という方法を使う。この方法は非常に強力で扱いやすいためにあらゆるところで使われている。
2.線形関数と線形近似
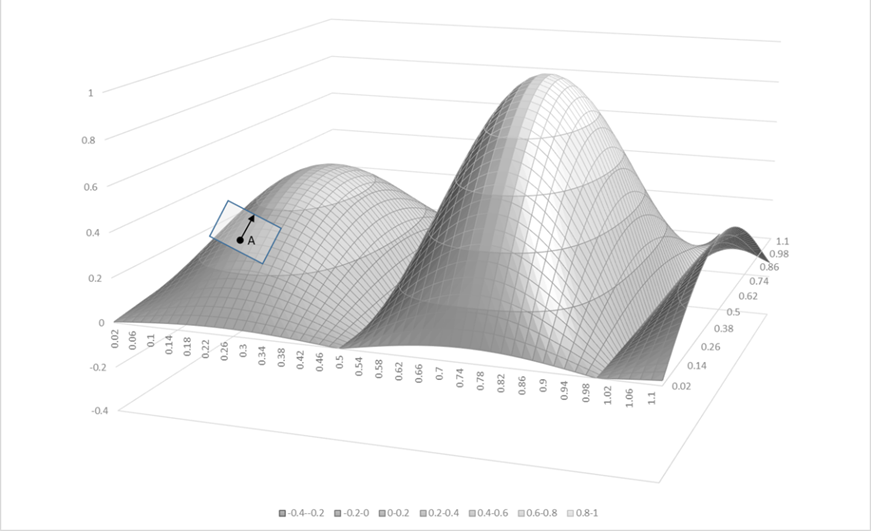
実際は、非線形の現象を線形で扱うためには線形近似という方法を使う。関数の線形近似とは簡単にいえば、関数をその点での接線(もしくは接する面、接平面)で近似するという考えである。
図Ⅲ-1-1は関数(曲面)と点Aで接している接平面を表している。曲面は大きく見れば曲がりくねっているが点Aの近くではだいたい平面に近くなるので、曲面の値の変わりにその点での接平面の値で近似しようという考えである。例えば、この曲面をあるチェーン店を経営している企業の「店の数\((x)\)」と「店舗の大きさ\((y)\)」に対する総売り上げを表しているものとする。現在は点Aにいるとする。このとき、将来総売り上げを上げるためには店の数と一店舗の大きさをどのように変化させればよいかを考える。このような問題に対しては、現在の点Aでの接平面を考え接平面の傾きが一番大きくなるような方向へ進めばよいと結論できる。しかし、この方法では、進むにつれて接平面と曲面の誤差が大きくなってしまう。そこで、少し進んだ時点で再度、接平面を求める。そして、新たな接平面で再度方向を決定することにより次の進む方向が決まるのである。
今、売り上げを決定する曲面があるとしてそれを近似するといったが、実際には曲面の形がどのようなものであるか分かることは稀である。しかし、線形近似法の強力な点は曲面の形が分からなくても行うことができることである。上記の例で言えば、ある時点において小さな実験(もしくは調査)を行うのである。すなわち、店舗数を少し増やしたり、店舗の大きさを少し大きくしたりして売り上げがどう変化するかを調査する。その小さな調査を多数行うと接平面の形がだいたい決まってくる6 。全体の曲面の形が分からなくても接平面を描くことは可能なのである。
事業活動における生産管理や品質管理などにおいてPDCA cycle(Plan-Do-Check-Action cycle)がある。これも、ある意味、線形近似による管理法であると考えてよいであろう。ある状態の事業において改善のためのプランを立て、それを実際に行い、改善が得られたかどうかを評価する。その評価に従いプランを微修正する。この繰り返しを行いながら全体を改善しようという作業である。これは、関数の頂上を目指すためにその点での接平面を構築し傾きが一番大きいところへ進み、少し進んだ段階で再度接平面を構築し進む道を見つける。これを繰り返していく。これは、まさにPDCA法の本質である。このように、PDCAサイクルというのも、非線形の現象を扱うための線形近似の方法なのである。
医療の領域でも線形近似が一般的に行われている。病気に対する原因などを調べるために比較試験が行われているが、これも線形近似の一種である。ある一つの変数(喫煙率など)を変化させて病気の発生率や死亡率がどのように変化するかを調べる。そして、その変数の変化と発生率などの変化に相関があれば、その変数が病気に影響すると判断する。これは、あくまでも局所的な有効性を調べているのである。例えば、煙草の健康被害がいわれているが、煙草を禁止すれば肺癌の死亡率は低下するかもしれない。しかし、全体の死亡率が低下するかどうかは分からない。また、医療費についてはどうかするという説もある。一般社会でも同じような方法はよく行われている。阪神が優勝したときの経済効果なども、線形近似と考えてよいだろう。
一方で、線形近似法はいくつか欠点を有している。その一つは、接平面と実際の曲面とのずれ(誤差)である。しかし、これは大きな問題ではない。上記のPDCAサイクルでもそうであるが、線形近似は一度で終わるわけではない。少し進めば再び線形近似を行い、ずれを修正することができるからである。ただ、医療などのように線形近似自体が大掛かりで莫大な費用がかかる場合には線形近似を繰り返し行うことが難しい場合もある。このような場合、ずれが大きくなった時点で事実が確立してしまうと、大きなずれを内包したままの事実が、そのまま踏襲されてしまう危険がある。
より大きな問題は線形近似で得られた解はあくまでも局所最適な解であり、大域的に見ればよい解ではないかもしれないという点である。地図なしで山登りをしていて、単に斜面の傾斜に従って登ってしまうと、目指す頂上ではない低い山の頂上に到達するかもしれない。また、頂上や底にある時には、接平面が水平になってしまうので、新しい解を見つけることが出来なくなってしまう。さらに、時には対象とする系が、突然の破壊であるカタストロフィーを起こす可能性もある。これらの可能性は線形近似の本質的な問題点である。
実はさらに深刻で重大な問題もある。それは、人間活動や生物学など相互に複雑な相互作用を行う系(複雑系)特有の問題である。曲面の頂上に向かって動くとその活動によって曲面そのものの形が変わってしまうという問題である[1][2]。これは、後に述べる複雑系などでは普通に起こる問題である。選挙予想をすると選挙結果が変わるという現象に似ている7 。これは問題自体が、線形近似になじまない(理論の破れ)と考えてよい。
このように線形近似の方法には大きな限界があるが、広域的な関数形が分からない段階(おそらく将来も分からない)では、この方法が間違っているとはいえないし、現実的にはこれに勝る方法は見つかってはいない。ただ、その方法の限界を常に意識しながら適用していくことが必要である。
3.力学系
次に変化方程式について考える。物理や数学の世界ではこのような時間変化を求めるための複数の変数から成る方程式系のことを力学系と呼んでいる(付録Ⅲ-1)。別に力学系といっても粒子の運動など物理的現象だけを問題にするわけではなく、社会の動き、経済の動き、生物数の変化なども扱われる。これらが、数学的にはすべて共通の微分方程式または回帰式で扱われる8。力学系という言葉は、最初にこのような方法を扱った力学への敬意の表れであろう。
力学系の方程式の解によって、系の時間変化が分かる。この時間変化を横軸に時間、縦軸に変数の値を書いたグラフによって時系列グラフが得られる。力学系の性質を時系列グラフで考えてもよいが、相空間という概念で考えるほうが分かりやすい。今、\(n\)個の方程式(その変数を\(x_1, …, x_n\)とする) からなる力学系が与えられたとき、各時点での変数の値を\(n\)次元の空間に \((x_1, x_2, …, x_n)\) という点で表したものを力学系の相図と呼んでいる。この時の空間の次元nを力学系の次元と呼んでいる。時系列データを直接表すより、力学系の性質がよくわかる。例えば、二つの変数\((x, y)\)からなる力学系の解が、\(x=sin(t), y=cos(t)\)である場合、これを相空間で表すと円になる(付録Ⅲ-2)。
世界をこのような時間変化を表す式で表すという考えはニュートンの力学に始まるが、目的は物事、対象の変化の関数を求めることである。前に関数の線形、非線形の話をしたが、そこで扱われる関数そのものを求める一つの方法が変化方程式である。このような考えがあったことで、初めて物理が自然科学の中心になることができたのである。
この変化方程式の考えは、いわゆる決定論的世界観というものを形作った。それは次のようのものである。すべての粒子の運動は微分方程式で表される。その微分方程式を解けば、将来の粒子の運動はすべて解明される。これは、世界の変化を完全に予測できることに等しい。
変化方程式においては線形と非線形では得られる時間変化の性質が大きく変わってしまう。そのため、線形近似の利用は限られたものになってしまう(理論の破れ)。線形の方程式の時間変化を表す解は完全に解くことができる(正確には定数係数の場合のみである)。時間変化の安定な最終の行き先(実際問題としてこれが重要なことが多い)は相空間で表すと、1)無限のかなたに去ってしまう、2)ある点に近づいて固定してしまう、の2つであることが分かっている。
安定というのは、自然にそこへ近づいていくという意味だけではなく、そこからずらしても、すぐにもとの点に戻るという意味である。前の事実は線形の方程式の場合は安定な状態が固定点かもしくは無限遠のどちらかしかないということを示している。振り子を例にして考えると分かりやすい、振り子は摩擦が無ければ一定の周期と一定の振幅で振れ続ける(周期運動)。ただ、この周期運動は不安定である。不安定というのはちょっと変動を与えるとすぐに他に移ってしまうという意味である。例えば、この振り子に少し力を加えて振幅を変えると、そのままで新しい振幅で振れ続ける。また、少しでも空気の摩擦があると、少しずつ振幅が小さくなり最終的には止まってしまう。現実の世界に全く摩擦が無いことはありえないので、振り子の遠い将来の状態は止まってしまう状態である。すなわち、この止まった状態は安定である。このように、線形の変化方程式では、無限のかなたに去る場合を別にして、安定な状態とは止まった状態のみである。
この静止の状態はいろいろなところに現れる。化学平衡、生体などのホメオスタシス(homeostasis)、フィードバックによる状態の安定化などのイメージはすべて振り子の静止した状態に似ている。しかし、実際の世界は変化に満ちている。線形の方程式ではこのような変化を説明することができない。
非線形方程式では状況は一変する。ここでも、過渡的な状態を除いた最終状態について考える。非線形方程式で最初に見つかった安定状態は周期運動である。振り子の場合は周期運動をしていても、すこしゆすってやるとすぐ別の振幅の運動に変化する。しかし、非線型方程式で見つかったこの周期運動は安定である。運動を少しゆすってずらしたとしても、すぐにもとの軌道に戻ってくる。その意味で、振り子とはずいぶん異なる運動である。ここで、初めて安定で変化する最終状態(定常状態)が見つかったのである。これは、リミットサイクル(limit cycle)と呼ばれている。
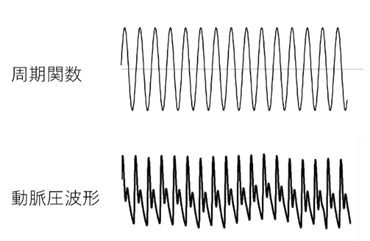
世の中に周期的に見える現象は多数ある。心臓の動き、呼吸運動などは一見、周期運動に見える。そのため、以前はこれらの運動はリミットサイクルではないかと考えられていた。しかし、心臓の動きにしろ、呼吸運動にしろ、よく見ると周期ではない(図Ⅲ-1-2)。一見周期的に見えるがよく見ると周期とは異なる運動。このような運動の原因はなかなか分からなかった。そのような中でカオスと呼ばれる状態が発見された。
カオス(chaos)というのは非線型方程式(微分方程式あるいは離散的力学系)の解の中に見つけられた非常に複雑な動きをする安定な状態のことである[3]。安定というのは一定の値に留まっているという意味ではない。ある一定の範囲内で非常に複雑な動きをしているが、その状態から少し 引き離しても再びそこへ戻ってくるという意味で安定なのである9。
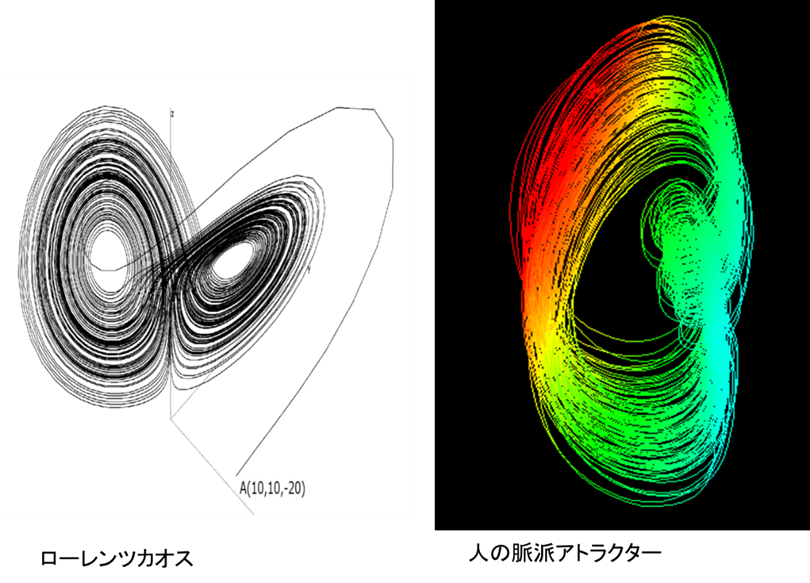
このように、動き続けていて周期でもなく引き離すとも戻ってくる状態を、あたかもその状態にひきつけられている奇妙な状態という意味で「ストレンジアトラクター(strange attractor)」(図Ⅲ-1-3)と呼んでいる(付録Ⅲ-2)。このようなカオス状態は一見すると周期運動のように見える。しかし、少し詳しく見ると周期とは異なる運動をしているのである。これらの動きは心臓や呼吸、脳波などの動きと似ておりこれらはカオス運動をしているのではないかと言われている。
4.カオスから複雑系へ
非線形方程式(連続系すなわち微分方程式あるいは離散力学系)に現れるカオス運動の特徴は以下のようである。
- (1) 時系列(軌道)は一見でたらめに見える。
単純な式からランダムに見える複雑な振る舞いが発生する。 - (2) 初期値鋭敏性:最初のどんな小さな誤差も大きく拡大される。
そのため、将来を予測することができない。カオスでは誤差の大きさは時間とともに指数関数的に増えていく。すなわち、誤差\(∝e^λt\) となる。この指数関数の係数\(λ\)(の平均)のことを「リアプノフ数(指数)(Lyapunov exponent、Lyapunov number)」と呼んでいる。この値はカオスを特徴づける重要な数である。この小さな変化が大きく拡大することを、「日本で蝶々が羽ばたけばアメリカに嵐が起こるかもしれない」と喩えて「バタフライ効果」と呼んでいる。
カオスは以上の性質をもつため、その状態を観察しようと、変化する軌道を丁寧に追いかけても意味が無い。その状態を観察し扱うためには、何らかの統計的扱いが必要になる。しかも、正規分布とは異なる統計的構造が見られる可能性がある。また、ストレンジアトラクターの幾何学的構造にはいわゆるフラクタル構造が見られることからカオスとフラクタルには関係があると見られている[4][5] 10。
代表的なカオスである。ローレンツカオスは次のような3つの変数からなる微分方程式で記述される。
\begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{dx}{dt}=-px+py \\
\dfrac{dy}{dt}=-xz+rx-y\tag{Ⅲ-1-6} \\
\dfrac{dz}{dt}=xy-bz
\end{array}
\right.
\end{eqnarray}
カオスが生まれるためには最低3つの変数からなる非線形の微分方程式が必要である。変数が二つの微分方程式から生まれるアトラクターは1点かリミットサイクルに限られることは証明されている(付録Ⅲ-2)。離散的な力学系では、ただ一つの方程式からもカオスが出現する。そのような最も簡単な方程式はロジスティックマップとよばれ \( x_{n+1}=ax_n (1-x_n )\) という方程式で記述される。
一般に、カオスは3,4個の方程式(方程式の変数の数を自由度と呼ぶ)で記述されるが、自由度が大きい系ではどのようなふるまいをするのであろうか。自由度が大きい系としては、気体が思い浮かぶ。気体はその粒子の数が\(10^{23}\)のオーダである。すなわち、自由度が\(10^{23}\)のオーダであるということである。このような多数の自由度からなる系は、数個の自由度からなる系と振る舞いがずいぶん異なってくる。気体の場合には個々の粒子の運動の特徴は失われてしまい、気体全体の対局的な振る舞いは、気圧(\(P\))、体積(\(V\)) 、温度(\(T\))という3つの変数でのみ表現することができ、有名な気体の状態方程式\(PV=nRT\)として表される。そこでは、多数の粒子の個性は無くなり、個々の粒子の運動は統計的な記述のみがなされる。すなわち、各粒子の運動エネルギーは正規分布に従い、個々の粒子の運動そのものは無視されていく。これは、個々の粒子の間の相互作用が小さいかほとんど無視されているためである。
では、非線型方程式で支配される自由度の大きい系でも、個々の変数の個性が失われて、何らかの巨視的な少数の変数で記述可能になるのであろうか。このような疑問に対して、津田、金子[2]等は多数の自由度を持つ単純な系を例としてこの問題を調べている。彼らは、微分方程式系では計算量が多くなるため、まず、多自由度の離散力学系の運動を調べた。具体的には、1自由度でカオスを発生する \(x_{n+1}=1-ax_n^2\) を基礎として、これを自由度\(N\)に拡張している。拡張の仕方によってCML(Coupled Map Lattice)とGCM(Globally Coupled Map)に分かれる。方程式で表すと、以下のようである。
\(f(x)=1-ax^2\) とし、時刻を\(n\)、変数番号を\(i\)とすると、それぞれ以下のN個の方程式で表される。
\begin{equation}
CML: x_{n+1}(i)=(1-\varepsilon)f(x_n(i))+\dfrac{\varepsilon}{2}(f(x_n(i+1))+f(x_n(i-1)) i=1, …,N \tag{Ⅲ-1-7}
\end{equation}
(ただし、\(x_n (N+1)=x_n (1), x_n (0)=x_n (N)\) とする)
\begin{equation}
GML: x_{n+1}(i)=(1-\varepsilon)f(x_n(i))+\dfrac{\varepsilon}{N}\displaystyle \sum_{i=1}^{N}f(x_n(i+1)) i=1, \ldots, N \tag{Ⅲ-1-8}
\end{equation}
CMLは各変数の値が両隣 \((i+1, i-1)\) にのみ影響を与える局所的な相互作用を表している。それに対して、GMLではすべての変数の値の平均が各変数に影響を与える大域的な相互作用を表している。定数εは影響を表す定数である。これが大きいと、他の変数への影響が大きくなる。GMLにおけるような大域的な影響は生物、社会などに多く見られる。例えば、血管系における血流を考えてみると、非常に簡単化したモデルでは各血管における血流はその血管にかかる血圧と血管抵抗で決まる。しかし、各血管にかかる血圧は全体の血圧の影響を受ける。全体の血圧は総血液量と全ての血管系から決まる全血管抵抗によって決まると考えられる。すなわち、個々の血管の血流はその部位の局所的な状況と大域的な全血流、全血管抵抗の影響を受けるという意味でGMLの要件を満たしている。
金子等は数百個の要素からなるGMLをシミュレーションした結果、いくつかの重要な性質を明らかにしている[2]。系はパラメータ\(a\)、\(\varepsilon\)の値によって、要素の全部あるいは一部が同期して振動する部分(アトラクター)に分かれる。具体的には次のどれかの状態を取る。
- 1)ほとんどすべての初期状態が完全に引き込んで振動する状態に落ちるコーヒレント相。
- 2)数個 (\(k<<N\)) のアトラクターが殆どを占める秩序相。各アトラクター内の要素はすべて同期し、時系列が同じになる。
- 3)初期条件により含まれる要素の数の異なるさまざまなアトラクターが共存する部分秩序相。
- 4)各要素が全くバラバラで振動する非同期相。
上記の1)~3)は自由度が減少するが、4)の場合は全部の要素がバラバラに動くので自由度は\(N\)のままである。最初の1)と2)の場合にはいくつかの部分に分かれて、それぞれの部分は同期して動く。そのため、この状態になるといつまでもこの状態が保たれる。元々は自由度がNであったものが\(k\)(普通は数個)にまで減少している。相図でいえば、数百次元のグラフであったものが、2次元(平面)や3次元(空間)のレベルのグラフにまで情報の圧縮が起こっているということである。次の3)の場合は複雑である。要素のうち、同期して動く部分に関しては1)、2)と同じである。しかし、それぞれが同期しないで動く部分を持っているのがこの状態の特徴である。同期しないで動く部分は、それぞれが全くばらばらというわけではなく、時間経過とともに、いくつかの要素がまとまって動いたり、またある時期には他の要素とまとまったりする。このように時間経過によってまとまった部分が変化する現象を津田、金子等は「カオス的遍歴(chaotic itinerancy)」と名づけている。低次元でのカオスの場合には一度できたアトラクターは変化しないでいつまでもアトラクターのままである。しかし、多次元の場合には、まとまった部分は一見アトラクターに見えるが、一時的なものであり、時間経過とともにそのアトラクターが崩れて全くばらばらになったり、他のアトラクターになったりする。いわば、アトラクター状態が安定状態ではなく準安定状態であるということである。
このような現象がカオス的遍歴である。時間経過の中でまとまった時期は自由度が低下している。しかし、バラバラの時期には自由度が大きくなる。そして、いつ準安定な状態が崩れるかは予測できない。シミュレーションの結果では、準安定状態からバラバラな状態への変化は突然起こるという結果である。これは、微視的な各要素の動きがカオス的であり、その軌道を完全に予測できないことに対応しているのであろう。また、この 3)の状態では、系の階層構造がしばしばみられるが、詳細は参考文献を参照してもらいたい。最後の4)の非同期相ではカオスになっていても個々の要素は別々に動いているため、自由度の低下は起こっていない。
後述するように、生体において多くのカオスが発見されている。それらの次元は多くの場合は数次元程度であり、数百次元という場合は見つかっていない。生体の多くは、数億万以上の次元から成り立つ力学系であると考えられる。そのような中で見つかっているカオスの次元が数次元であるということは、GMLの研究で見つかっている次元の縮約が起こっていると考えられるのであろう。次元のこのような低下はある意味、要素間の相互作用によって系の中に一つの秩序が現れているとみてもよいのであろう。
第2章 複雑系とベキ分布
1.ベキ分布とは
カオス理論は力学系の理論から見つけられた。その際、力学系の自由度(方程式の数と考えて良い)は3,4程度であった。自由度が少ないということは、系がある意味単純であるということを意味している。では、より多数の自由度からなる系、多数の要素からなる系ではどうなるかという疑問が生まれる。その問いに対して答えたのが第1章-4で説明した、多数の要素からなる力学系の理論である。多数の要素からなる系は当然多数の自由度を持つ系である。CMLやGMLなどはまさに、多数の要素(自由度)から成る系の例である。CML、GMLの研究からわかったことは、このような系においても少数自由度のカオス理論と同じような状態が生まれるということである。すなわち、系全体が周期運動をしたり、小さな自由度のカオス状態に陥ったりするということである。しかも、このような状態が一つの系に多数存在するという特徴がある。そのため、系の初期条件の違いによって、異なる状態に落ち着いていく。さらに重要な点は落ち着いた先が一見安定なように見えるが、時には急にその状態が崩れ、他の状態に移行することがあるということである。系の中には多数の準安定な状態があり、時間の経過とともに準安定な状態間を遷移していく。これが多数自由度の力学系で見られる現象である。
カオス理論から生まれたもう一つの重要な点は、系の記述法である。もともとのニュートン力学では、系はそれに含まれる粒子の位置とその時間変化によって表される。ニュートン力学というのは位置の変化を予測、それも完全に予測する理論、いわゆる決定論である。しかし、カオス理論によって位置を完全に予測することは不可能であると証明された。このことは、系を記述するのにそこに含まれる粒子のある時刻の位置を確定するという方法が不可能であるということを意味している。では、その場合、系はどのように記述すればよいのであろうか。カオス理論によれば、位置を完全に決めることは出来ないが、要素の位置の確率は決めることができる。すなわち、系の記述法としてある時刻の位置から位置の確率に変化するということである。このことは、CMLやGMLなどにおいても同じことである。系の要素の正確な値を記述することに意味はなく、要素の値の確率分布、場合によっては系全体を表す指標の確率分布を予測することしか出来ないということである。
さらに、もう一つの重要な点は、階層構造である。CMLやGMLの研究から、準安定状態に階層構造がみられるとのことである。力学系以外の世界では階層構造がみられるのは当たり前と言えば当たり前であるが、力学系の中からも階層構造がみられるのは重要な事実である。もともと物理の世界でも、小さな質点の力学に対して、多数の質点から成る統計力学という世界がある。統計力学の世界は質点の力学に比べ確率の世界である。またその世界を表現する方法も微視的世界とは異なり、統計的な平均を表す温度、圧力、エントロピーなど巨視的な指標で記述される。かつては、微視的力学の方法で巨視的な世界の法則を説明しようとしたが、結局失敗に終わっている。微視的な世界と巨視的な世界という階層が世界にあり、下の階層の論理で上層の階層の理論を証明することは出来ない。ニュートン力学、あるいは、現在では量子力学によって巨視的な世界を記述することは不可能であるということである。これは巨視的な世界には巨視的な論理が必要であることを意味している[2]。
力学系で表せる世界のより上位の階層には力学系で表せない世界や対象が多くある。生物の世界、特に生物の集団の世界に関しては力学系で表せる対象は少ない。個体数、病気の感染の広がりなどはある程度、力学系で表される。しかし、個体の行動、個体が集まった社会的行動、ましてや人間社会、人間が作る社会などは力学系で表すことはほとんど不可能である。では、このような世界には一般的な法則は存在しないのであろうか。このような問いから複雑系の概念が生まれた。
複雑系というのは定義がまだ定まっていないため、人によって定義が異なっている。しかし、おおむね次のような定義が一般的である。
- 1)システム11は多数の要素(エージェント12)によって構成される。
- 2)各エージェントは互いに局所的な相互作用を行う。
- 3)この局所的な相互作用によって各エージェントの性質からは予測できない全体の性質・状態・振る舞いが出現する。
- 4) この全体的な性質・状態・振る舞いが個々のエージェントの振る舞いに影響を与え、個々のエージェントの振る舞いが変化する。
ここで、3)、4)は1)、2)によって自動的に決まってくるものであり、最初からこのような全体を表す状態が存在するわけではない。
システムの要件は1)、2)であるが、単にこれだけを満たすものを複雑系といっているわけではない。1)、2)で構成されたシステムから3)で示されるような全体の状態が自然に出現する場合がある。これを「創発(emergence)」と呼び、このようなシステムを複雑系と呼んでいる。ここで、4)についてであるが、3)のような全体の性質が出現したとしても、個々のエージェントの振る舞いが変わるわけではない。あくまで個々のエージェントは最初から決まっている局所的な相互作用を行っている。しかし、外から見たときにはその動きがあたかも全体の性質に影響されたように見えるという意味である。物々交換をしているようなモデルをシミュレーションすると物々交換している品物の一つがあたかもお金のような働きをするという報告がある[6]。この際、各エージェントはあくまでも物々交換をしているのであるが、結果としてある決まった品物を介して物々交換しているように見えるということである。そして、個々のエージェントの行動がお金を介する行動として説明できるようになる。これは個々の局所的な相互作用によってお金が創発したと考えることが出来る現象である。
上記の定義で2)の局所的な相互作用については、いささか注意が必要である。厳密な意味での局所的という意味は、時間的にも空間的にも局所という意味である。すなわち、あるエージェントのある時刻の性質がすぐ近くの他のエージェントにのみ影響を与えるという意味である。しかし、このような意味の局所相互作用で全体的な性質が出てくるかどうかははっきりしない。前述のGMLは相互作用の中に全体の平均という大域的な性質を含ませている。全体の平均というのは各エージェントの性質が全体に影響しているということである。全体の秩序が生まれるという意味での複雑系が成り立つためには、各エージェントの影響範囲が空間的あるいは時間的に大域的である必要があるかもしれない。人間社会を含む生物集団の場合には、記憶という性質によって個々の相互作用が大域的な相互作用になっていると思われる。
このような、複雑系の特徴としては次のようなことが言われている。
- 1)全体を要素に分けて分解しても全体の理解はできない。
- 2)部分の性質の単純な総和にとどまらない性質が全体として出現する。
- 3)原因と結果は一意的には結びつかない。
- 4)現在の状況や現象は過去のすべての現象に影響される。
- 5)系の変化、現象の変化は長期的には予測できない。
複雑系は非線形数学とくにカオス系から生れてきた概念である。そのため非線形系の性質を引き継いでいる。上記の内容のうち、3)、4)、5)はカオス系での初期値鋭敏性から導かれる事実である。さらに、2)は創発の概念であり複雑系にとって本質的である[7][8][9]。
第1章で述べた気体の場合は、多数の自由度であるが互いに小さな相互作用をしている系である。粒子ごとの相互作用は各粒子のエネルギーの交換を行い、最終的に粒子の運動エネルギーは平均エネルギーのまわりに分布する正規分布となる。この平均エネルギーが気体の状態を表す重要なパラメータである温度になる。温度が気体の性質を代表する重要なパラメータであるのはエネルギー分布が正規分布をするからである。この場合、温度という性質は各エージェントの性質から予想されない性質ではない。単に個々の粒子のエネルギーの加算に等しいからである。これは、まさに全体を細かい要素に分解し、全体を理解するためにはそれを単純に加算したものであり、部分をたしていけば全体を表すことができる、という考えに一致する。このように、気体は多数の要素から成り立っているが複雑系とはいえないシステムである。
エージェント間に相互作用があるとどのようなことが起こるのであろうか。コインの裏、表を当てるゲームを考える。コインを投げて、多数の人に裏か表を当てさせる。まず、いま、この多数の人が一列に並んでいると考える。そして、順番に裏と思うか表と思うかを聞いていく。このとき、他人がどのように答えたかを教えないで聞いた場合と、隣の人がどのように答えたかを教えてから聞いた場合の二つを考える。おそらく、最初の例では答えの列はいわゆるランダム列になるであろう。しかし、次の例では各人は隣の人の答えの影響を受けて答えるため、ランダム列にならない可能性がある。このように、相互作用があると、ランダムからずれてくるのである。
複雑系一般に成り立つ性質があるかどうかは分かってはいない。しかし、先ほどの気体での正規分布に対応するものとして複雑系ではベキ分布と呼ばれる分布がしばしば見られる[9][10]。ベキ分布というのはある変量の頻度分布(確率分布)が1/xαに比例する分布である。ベキ分布の性質などは以下の章で詳しく述べるが、医療以外にも表Ⅲ-2-1、図Ⅲ-2-1に示すように多くの複雑系において見られる。特に最近は、多くのベキ分布がインターネット上に出現することが知られている。ネットワーク上のベキ分布は「複雑ネットワーク」として知られ、最近の重要なトピックである[11]。

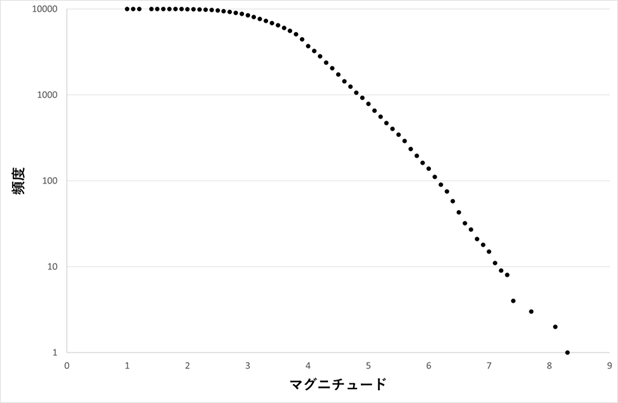
気象庁地震データベースのデータから筆者が作成。
マグニチュードマグニチュード4以上のところで、
マグニチュードとその頻度の対数が直線関係であるのが分かる。
マグニチュードが4以下のところでは直線関係が崩れる。
従来、多くの統計的現象は正規分布になると信じられてきた。また、現象を説明するために正規分布を仮定して理論を構築することが多かった。ベキ分布をする系を正規分布で近似した場合には実際の値との間にずれや漏れが生じる。この漏れは想像以上に大きく、正規分布を仮定した理論による予想が崩れたり、理論構築そのものが崩壊する場合もある。最近起こった金融危機の要因は、金融工学という理論において為替変動が正規分布をすると仮定したために市場の大きな変動を予測できなかったためであるという説も存在する。実際には為替の変動も正規分布からずれたベキ分布に近い分布をするといわれており、複雑系的な解釈が可能であると思われる[9]。
ベキ分布は別名「スケールフリー分布」もしくは「フラクタル分布」などとも呼ばれフラクタルやカオス系と深い関係があると考えられている。ベキ分布がなぜ起こってくるかについては、多くのモデルが提案されている。そのいくつかは以下の章で論じる。
2.ベキ分布の原因
複雑系においては、各要素の相互作用により、各要素のふるまいからは予測できない全体の性質が出現する。そのような性質で最もしばしばみられるのがベキ分布を代表とするすそ野の長い分布である。「ベキ分布」は文章の中の単語の頻度、相転移などの物理現象、生物における細胞レベルの現象、生物集団における現象、人間社会の現象など非常に広範にみられる[12][13][14][15][16][17]。
2-1 ベキ分布、すそ野の長い分布
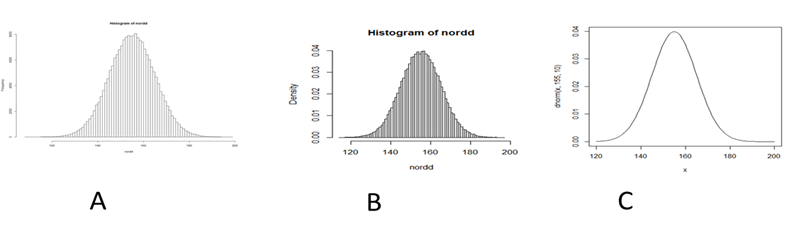
図Ⅲ-2-2のAをある仮想的な集団100000人(\(N\)とする)から作った身長のヒストグラムと考えよう。刻みは1cmであるとしよう。この時、この集団から無作為に一人を選んだ時、その人の身長が140cmから141cmである確率は、グラフの140cmから読み取った頻度を\(a\)とすると、\(a/N\)である。そこで、直接確率を表すようにするにはAのグラフの縦軸をすべて\(1/N\)倍すればよい。これが、グラフのBである。このグラフからは直接、ある身長である確率を読み取ることができる。しかし、この図は刻みが1cm毎である。そのため、140cmから140.5cmである確率を読み取ることができない。その場合はヒストグラムの刻み間隔を小さくしていく必要がある。しかし、刻み間隔を小さくするとグラフの誤差が大きくなっていってしまう。誤差を小さくするには測定する集団を大きくしていく必要がある。結局、集団の大きさをどんどん大きくし、同時に刻みの間隔を小さくしていくと、グラフはなめらかな曲線になる。この曲線がグラフCである。
このような確率を表すなめらかな曲線を確率密度関数(probability density function, PDF)と呼んでいる。確率密度関数 \(p(x)\) の意味は値 \(x\) を取る確率変数 \(X\) の値13 が \(a\) 以上、\(b\) 未満、すなわち \(a\leq X \lt b\) である確率が \(p(x)\) の曲線の \(a\) から \(b\) までの面積 \( \int_{a}^{b}p(x)dx\) となる曲線という意味である。もしくは、\(dx\) を小さな値としたときに \(X\) が \(x \leq X \lt x+dx\) である確率が \( p(x)dx \) となるという意味である。この確率密度関数の代わりに分布関数(distribution function、あるいは累積分布関数 cumulative distribution function, CDF)を使う場合もある。分布関数を \( F(x) \)とすると、これは、\( p(x) \) のグラフにおいて \( x \) 以下の面積という意味である。すなわち
\begin{equation}
F(x)= \int_{- \infty}^{x} p(x)dx=P(r) (X \leq x) \tag{Ⅲ-2-1}
\end{equation}
である14。すなわち、\(X\) が \(x\) 以下となる確率という意味である。累積分布関数の代わりに相補累積分布関数(complementary cumulative distribution function:CCDFあるいはCCD) \( CF(x) \) を使う場合もある。これは
\begin{equation}
CF(x)=\int_{x}^{\infty} p(x)ds=Pr(X \gt x)=1-F(x) \tag{Ⅲ-2-2}
\end{equation}
と定義される。すなわち、Xがxより大きくなる確率という意味である。確率を考える場合にPDF、CDF、CCDF(CCD)のどれを使ってもよいが、何を使っているかを意識することが必要である。
確率変数 \(X\) あるいは \(p(x)\) がベキ分布をなしているとは、\(x\) がある値 \(x_{min}\) 以上であるときに \(p(x) \)が \(x^{-\alpha}\) に比例する場合をいう。すなわち
\begin{equation}
p(x) \propto \frac{1}{x^{\alpha}} (x \gt x_{min}) \tag{Ⅲ-2-3}
\end{equation}
となる時に \(p(x)\) はベキ分布に従うという。 比例関係は\(x \gt x_{min}\) の時のみに成り立てばよい。このことはベキ分布というのは \(x\) の大きい場所(すそ野)での現象であることを示している。
ここで、\(\alpha\) のことを「べき指数」と呼んでいる。(Ⅲ-2-3)の両辺の対数を取ると
\begin{equation}
p(x) \propto \frac{1}{x^{\alpha}} (x \gt x_{min} \tag{Ⅲ-2-4}
\end{equation}
となる。これにより、値 \(x\) の対数とその確率の対数をグラフにとると直線になることが分かる(図Ⅲ-2-3)。確率の代わりに頻度でも同じである。この直線の傾きから \(\alpha) \)を求めることができる[18]15。
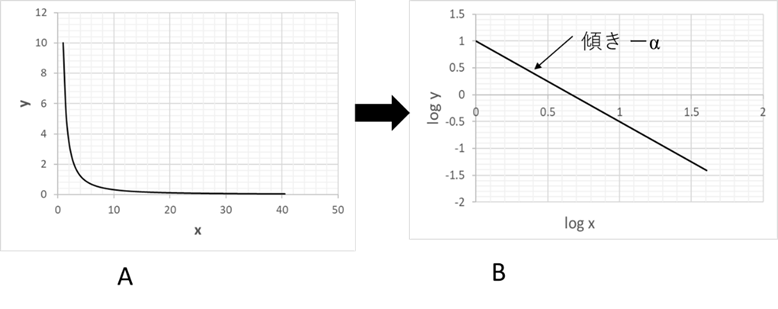
A:ベキ分布図、B:両対数グラフ
実際のデータから、ベキ分布をグラフで表現するのには確率密度以外にZipfプロットやCCDFの方法がある。それらの相互の関係については付録Ⅲ-4を参照してもらいたい。ZipfプロットやCCDFにおいても、ベキ分布の場合は両対数グラフで直線になる。同じデータに対するZipfプロットの両対数グラフの傾きを \(-\zeta\)、CCDFの両対数グラフでの傾きを \(-β\) とすると、次の関係がある(付録Ⅲ-4)。
\begin{equation}
\alpha = \beta +1=\frac{\zeta +1}{\zeta} \tag{Ⅲ-2-5}
\end{equation}
今後は確率密度にけるべき指数 \(\alpha\) を単にベキ指数と呼び、ZiPfプロットの傾きから求めた指数はZipfs 指数(あるいは単に \(\zeta\) )、CCDFのグラフの傾きから求めた指数は \(\beta\) と呼ぶことにする。
ベキ分布というのは本来、確率分布の話である。しかし、確率分布に限らず二つの変数 \(y\) と \(x\) がベキ関係で結ばれていることがある。すなわち、
\begin{equation}
y \propto \frac{1}{x^{\alpha}} \tag{Ⅲ-2-6}
\end{equation}
となる場合である。この場合はyとxには「ベキ乗則」(power law)の関係があるという。またここでも \(\alpha\) のことを「ベキ指数」と呼ぶ。「ベキ分布」は確率と \(x\) には「ベキ乗則」の関係がある分布と言い換えることもできる。
ベキ分布が複雑系において注目される理由は、一つは複雑系でしばしばみられることである。もう一つは、ベキ分布は正規分布などとは大きく異なる性質を持っていることである。ベキ分布の特徴はベキ指数 \(\alpha\) の値によって異なる。数学的には次の3点である。
① \(0 \leq \alpha \leq 1\)
\(\alpha =1\) の場合は
\begin{equation}
\int_{x_{min}}^{\infty} p(x)dx=\int_{x_{min}}^{\infty} \frac{A}{x} dx=[A \log x]_{x_{min}}^{\infty}= \infty \tag{Ⅲ-2-7}
\end{equation}
\(\alpha \leq 1\) の場合は \(\displaystyle \frac{1}{x^{\alpha}} \geq \frac{1}{x} \) なので、やはり上の積分は発散する。結局、この場合 \(p(x)\) は確率分布にはならない。
② \( 1 \lt \alpha \leq 2 \)
この場合、\( \int_{x_{min}}^{\infty}p(x)dx \) は有限の値になるので、\( p(x) \) は確率分布となる。しかし、
\begin{equation}
\int_{x_{min}}^{\infty}xp(x)dx=\int_{x_{min}}^{\infty}xA/x^{\alpha}dx= \int_{x_{min}}^{\infty}A/x^{\alpha -1}dx \tag{Ⅲ-2-8}
\end{equation}
となり、\( \alpha -1 \leq 1 \) となるので、上記の積分は発散する。すなわち平均が存在しなくなる。
③ \( 2 \leq \alpha \leq 3 \)
上記と同じ議論で、平均は存在するが分散が無限になる。これは、データのばらつきが非常に大きいことを示している。
以上のように、ベキ分布はそのベキ指数の大きさによって、\( p(x) \) の振る舞いが大きく異なる。
医療においてこのことがどのような影響を与えるかについては3章において改めて述べる。
医療を含めた社会現象においては、ベキ分布以外にも多くのいわゆる「すそ野の長い分布」(long tail distribution) と呼ばれる分布が存在する。対数正規分布(lognormal distribution) あるいは切り捨てベキ分布 (truncated power-law distribution) がその代表である。これらは、すそ野に関して大きな違いはない。実際には、ベキ分布であるといわれている分布も、正確には \( x \) の大きいところではベキ分布から外れる場合が多い。そのため、ベキ分布といっても実際は平均値、分散は存在する。ただ、いずれの分布においても非常に大きな分散になるため、応用上はあまり大きな差はないであろう。
2-2 ベキ分布の成因
そのようなベキ分布を作るメカニズムについては多くのモデルが提案されている[19]。Newmanによれば、ベキ分布のメカニズムとして次のようなものが存在する。
- 1)指数関数の組み合わせ
- 2)逆数
- 3)Random walk model
- 4)Yule process (rich-get-richer)
- 5)相転移
- 6)Self-organized criticality
- 7)折れ棒モデル
上記のうち、1)、2)はある面トリッキーなメカニズムである。「指数関数の組み合わせ」とは次の様にして起きるベキ分布である。もし、ある量 \( y \) が指数分布をするとする。すなわち、\( p(y) \sim exp(ay)\) (\( p(y)\) は\( y\) の確率密度)の関係がある。さらに、量 \(x\) が \(y\) と \(x \sim exp(by)\) の関係があるとする。すると、\(x\) の分布 \(p(x)\) は
\begin{equation}
p(x) \propto \frac{x^{-1+ \frac{a}{b}}}{b} \tag{Ⅲ-2-9}
\end{equation}
となる。すなわち、ベキ指数 \(\alpha = 1-a/b\) のベキ分布となる。
二つ目の「逆数」というメカニズムは、\(y\) の分布 \(p(y)\) が \(p(0)>0\) となるとき、\(x=1/y\) となる、\(x\) を考えると、
\begin{equation}
p(x)=p(y) \dfrac{dy}{dx} = -\frac{p(y)}{x^2} \tag{Ⅲ-2-10}
\end{equation}
となる。ここで、\(x\) の大きいところでは \(y\) はゼロに近くなるので、結局 \(p(y) \simeq p(0)\) となるので、
\begin{equation}
p(x) \simeq \frac{p(0)}{x^2} \propto x^{-2} \tag{Ⅲ-2-11}
\end{equation}
となる。
これは、ある意味、見かけのベキ分布との考えられる。これら二つのベキ分布のメカニズム以外の4つについては重要であるので少し詳しく述べよう。
これは、色々なものの寿命のモデルとして考えられたものである。Random walk modelというのは次のようなモデルである。
時刻 \(n\) における状態 \(x(n)\) が整数 \((…, -2, -1, 0, 1, 2, …)\) で表せるとする。
このとき、各時刻で確率 \(p\) で+1、\((1-p)\) で-1変化する。
すなわち、
\begin{eqnarray}
\left\{
\begin{array}{l}
x(n+1)=x(n)+1 確率 p \\
x(n+1)=x(n)-1 確率 (1-p) \tag{Ⅲ-2-12}
\end{array}
\right.
\end{eqnarray}
で変化する。
この時、\(x(0)=A\) として、最初に \(x(n)=0\) となる \(n\) をこのシステムの寿命 \(T\) と考える。
このモデルで、\(p=1/2\) の場合には、\(T\) の分布はベキ分布になる[20]。具体的には、
\begin{eqnarray}
p(T) \propto T^{-1.5}
\end{eqnarray}
となる。すなわちベキ指数 \(\alpha =1.5\) のベキ分布となる。このモデルを少し変形すると、入院期間の分布についてのモデルを作ることができる(詳しくは第3章)。
これは別名 rich-get-richer (富める者はさらに富む)といわれるモデルである。このモデルで説明される現象としては、都市の人口分布、論文の引用件数の分布、生物分類中の属に含まれる種の種類の分布、web の links の分布などがある。あとで述べるが、医療における病名の患者数の分布もこのメカニズムが関係していると思われる。
ここでは、都市の人口分布のモデルを紹介しよう。都市の人口分布はベキ分布を成すことは良く知られている[8]。これを説明するためのモデルが Yule processである。モデルは次のようなものである。
いくつかの都市からなるシステムに対して
- 1.定期的にある一定の人口の群がこのシステムに加わる。
- 2.群は確率πで新しい都市を作るか、確率1-πですでに都市を形成している集団に加わる。
- 3.集団が既存の都市に加わる場合、どの都市に加わるかの確率は、各都市の人口に比例する。
これだけである。図Ⅲ-2-4 はこのモデルをシミュレーションした結果である。
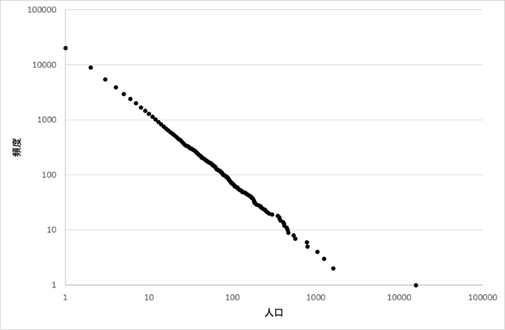
グラフを見ればわかるように、都市の人口がベキ分布をしていることが分かる。この簡単なモデルはすでに述べたように多くの「ベキ分布」を起こす現象のメカニズムとして使われている。
相転移とは本来は物理現象である。系の状態が急激に変化する状況を表している。水がある温度で氷になったり気体になったりする現象である。相転移を起こさない時点では、系には固有のスケール(長さ、サイズ、タイム)などがあるという。しかし、この固有のスケールが相転移を起こす正にその時点(critical point) で失われる現象が起こる。そのcritical pointではありとあらゆる長さやサイズが起こり、その長さの分布が「ベキ分布」をなす。
相転移はある特定の温度や環境の時に起こる特殊な状況である。そのため、稀にしか起こらない現象と考えられる。それに対して、自己組織化臨界現象というのは、システムの性質として自動的にそのようなcriticalな状態を作り出すという現象である。この現象はPer Bakが相転移の研究の中で見つけた概念である[7][21]。彼の作ったモデルは「砂山崩しモデル」といわれている。砂を地面に少しずつ積み上げて行くと、ある時点でもう積み上がらないようになり雪崩が起きる。この時点での雪崩の大きさの分布がベキ分布を成すというモデルである。このモデルは、地震におけるマグニチュードとその頻度の関係(グーテンベルク・リヒター則 図Ⅲ-2-5)、山火事の大きさとその頻度の関係などを説明するモデルとして利用されている。医療の世界では今のところこのモデルで説明できる現象は見られないようである。しかし、後で「切り捨てベキ分布」の概念の説明で重要になるので、ここで、このモデルの説明をしておく。このモデルは次のようなものである。
一辺Nの格子を考える。
- ① 各時点で一つのブロックをランダムな場所におとす。
- ② 落とした結果、落とされた格子のブロックの数が4になれば、その格子の周り4つの格子に一つずつブロックを配分(雪崩)する。
- ③ 配分された格子のブロックの数が4であれば、その格子に対して②を行う。この操作を雪崩が止まるまで繰り返す。雪崩が止まれば、①へ戻る。

左上の格子から始まる。左上の格子の真ん中の格子にブロックが落ちる。
すると順番に雪崩が起こり、右下で止まる。雪崩の大きさは7である。
このモデルでは格子の大きさは無限であると考えている。格子の大きさが無限であるとした場合のみ完全なベキ分布が得られる。有限とした場合にはあとで述べるように「切り捨てベキ分布」が得られる。
2-3 ベキ分布以外のすそ野の長い分布
対数正規分布
ベキ分布はすそ野の長い分布である。すそ野の長い(long tail)という意味は図Ⅲ-2-6を見ていただきたい。この図のAは正規分布とベキ分布を並べて書いたものである。この図を見れば、一見、ベキ分布は急激に減少し、正規分布はゆっくり減少しているように見える。しかし、この図で \(x=1000\) 以後を拡大したものがBである。この図を見ると、ベキ分布が正規分布よりゆっくり減少しているのが分かる。このように、\(x\) が大きい場所(すそ野)においてベキ分布は正規分布などに比べてゆっくり減少していく。このようにすそ野においてゆっくり減少する分布を「すそ野の長い分布」と呼んでいる。
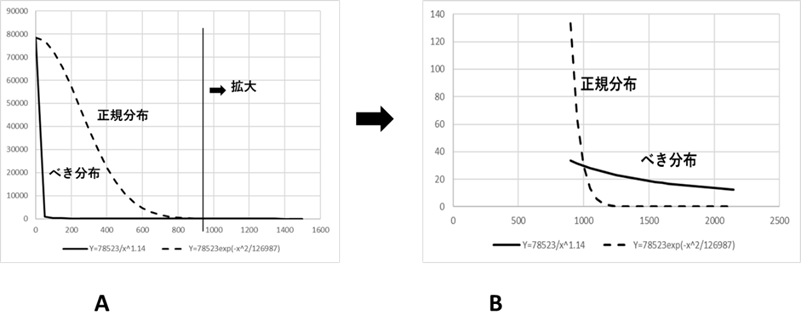
A:元の図、B:図Aのすそ野を拡大したもの
「すそ野が長い分布」はベキ分布だけではない。ベキ分布以外の「すそ野の長い分布」としては、対数正規分布(lognormal distribution)、対数ロジスティック分布(loglogistic distribution)、逆ガウス分布(inverse Gaussian distribution)などが知られている。以下にそれぞれの確率密度関数を示す。
その対数が正規分布をするような確率変数という意味である。
\begin{eqnarray}
p(x)=\frac{1}{\sqrt{2 \pi} \sigma x}\exp \displaystyle\left ( -\frac{(\ln x- \mu)^2}{2 \sigma^2} \right ) \tag{Ⅲ-2-13}
\end{eqnarray}
\begin{eqnarray}
p(x)=\frac{\exp \displaystyle\left (-\frac{\ln x-\mu}{\sigma}\right )}{\sigma x \displaystyle\left (1+\exp \displaystyle\left (-\frac{\ln x-\mu}{\sigma} \right )\right )^2} \tag{Ⅲ-2-14}
\end{eqnarray}
\begin{eqnarray}
p(x)=\displaystyle\left(\frac{\lambda}{2 \pi x^3} \right)^{\frac{1}{2}} \exp \displaystyle\left(-\frac{\lambda (x-\mu)^2}{2 \mu^2 x} \right) \tag{Ⅲ-2-15}
\end{eqnarray}
これらの分布は、生存時間解析によく使われる分布である[80][98]。これらはいずれもすそ野は長いがベキ分布とは異なり、平均、分散が常に存在する。ベキ分布と比べると、両対数グラフで見た確率密度関数が \(x\) の大きいところで直線から下へずれるのが特徴である(図Ⅲ-2-7)。
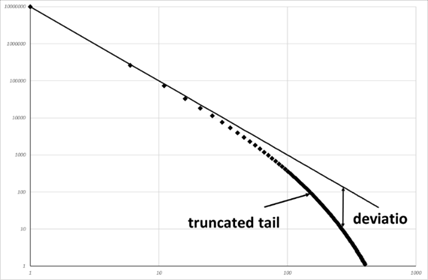
これらの中で対数正規分布は複雑系において、ベキ分布とともによく見られる分布である。金子は第2章で述べた多数の要素からなる力学系の応用として、多数の物質の化学反応の数学モデルにより細胞分裂、細胞の進化の問題を論じている[26]。その中で、彼はこのモデルの結果の中にしばしば「ベキ分布」と対数正規分布が出現すると述べている。一般に、化学反応による量の変化は、だいたい、各成分の量の積に比例して増える。その結果として対数正規分布が生まれると述べている。このことをもう少し詳しく述べておく[27]。
ある量の時刻iにおける量がXiで表されるとする。このとき、\(X_i\) が次の式によって時間変化をするとする。
\begin{eqnarray}
X_i=\alpha_{i-1}X_{i-1} \tag{Ⅲ-2-16}
\end{eqnarray}
ここで、\(\alpha_{i-1}\) は各時刻によってランダムに変化する値(確率変数)だとする16。この量の最初の値を\(X_0\) とすると、時刻 \(n\) での値は
\begin{eqnarray}
X_1=\alpha_0 X_0 X_2=\alpha_1 X_1=\alpha_1 \alpha_0 X_0
\end{eqnarray}
以下同様にして
\begin{eqnarray}
X_n=\alpha_{n-1} \alpha_{n-2} \ldots \alpha_0 X_0
\end{eqnarray}
この両辺の対数を取ると
\begin{eqnarray}
\ln X_n=\ln X_0 + \ln \alpha_{n-1} + \ln \alpha_{n-2} + \cdots + \ln \alpha_0 \tag{Ⅲ-2-17}\\
\ln \frac{X_n}{X_0}=\ln \alpha_{n-1} + \ln \alpha_{n-2} + \cdots + \ln \alpha_0 \tag{Ⅲ-2-18}
\end{eqnarray}
ここで、\(n\) が非常に大きい時には、上式の右辺は中心極限定理により正規分布をする。すなわち、\(\ln \alpha_i \) の平均値を \(\mu_i\) 、分散を \(\sigma_{i}^2\) とし、\(m_n=\sum_{0}^{n-1} \mu_k\)、\(s_n^2=\sum_{0}^{n-1} \sigma_{k}^{2}\) とおく。
さらに、\(y_n=\ln X_n\) とすると、この \(y_n\) が正規分布をする。
\begin{eqnarray}
p(y_n)dy_n=\frac{1}{s_n \sqrt{2\pi}} \exp \displaystyle\left (-\frac{(y_{n}-m_{n})^2}{2s_n^2} \right )dy_n\\
=\frac{1}{s_n \sqrt{2\pi}} \exp \left (-\frac{(y_{n}-m_{n})^2}{2s_{n}^2} \right )\frac{dy_n}{dX_n} dX_n\\
=\frac{1}{s_n \sqrt{2\pi}} \exp \left (-\frac{(\ln X_{n}-m_{n})^2}{2s_{n}^2} \right )\frac{1}{X_n} dX_n \tag{Ⅲ-2-19}
\end{eqnarray}
結局、\(X_n \) の確率密度 \(p(X_n)\) は
\begin{eqnarray}
p(X_n)=\frac{1}{s_n X_n\sqrt{2\pi}} \exp \left (-\frac{(\ln X_{n}-m_{n})^2}{2s_{n}^2} \right ) \tag{Ⅲ-2-20}
\end{eqnarray}
となる。
医療の中には多くの「ベキ分布」あるいは「すそ野の長い分布」がよくみられる。それらについての発生メカニズムについては第5章で改めて述べる。
切り捨てベキ分布
「すそ野の長い分布」としてのもう一つのタイプは、ベキ分布から生成されるタイプである。ベキ分布に比べてxが大きいところでベキ分布より急激にゼロに近づくタイプである(図Ⅲ-2-7)。分布の形としては
\begin{eqnarray}
p(x) \propto x^{-\alpha}F(x/x_0) \tag{Ⅲ-2-21}
\end{eqnarray}
ここで、
\begin{eqnarray}
F(x)=
\left\{
\begin{array} {l}
1 for x \lt 1 \\
\exp{(-ax)} for x \geq 1
\end{array}
\right.
\end{eqnarray}
\(\alpha\)、\(x_0\)、\(a\) は定数である。特に \(\alpha\) はベキ分布のベキ指数に対応する。
この切り捨てベキ分布(truncated power-law distribution)はベキ分布を作り出すメカニズムに何らかの制限をつけると生まれる。例えば、砂山崩しのメカニズムを考える。砂山崩しのモデルにおいては、一辺Nの格子を考えた。実は砂山崩しモデルにおいて、完全なベキ分布を生み出させるためには一辺が無限でなければならない。その意味で、このモデルには最初から制限がついている。このことを示したのが図Ⅲ-2-8である。図は格子サイズが10×10である砂山モデルをシミュレーションした結果である。図のA、B、Cはそれぞれ、シミュレーション回数を1000、2000、10000とした図である。シミュレーション回数が2000までは頻度分布の直線性がよく保たれている(ベキ分布性が保たれている)。しかし、シミュレーション回数が10000の(C)では、サイズの大きい所でグラフは下の方に傾き、頻度分布の直線性が失われている。これは、モデルの格子サイズを10に制限したためであり、得られた結果は切り捨てベキ分布を示している。
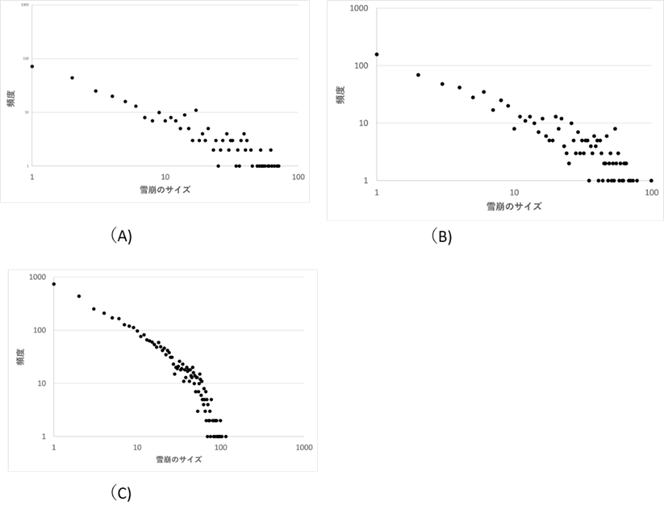
A:計算回数 1000、B:計算回数 2000、C:計算回数 10000
都市人口モデル(図Ⅲ-2-4)においても、制限を掛けると切り捨てベキ分布が得られる。図Ⅲ-2-9は都市人口モデルのシミュレーション結果である。図の(A)は制限のない場合、(B)は都市の数が1000に制限されている場合である。モデルの(B)においては、都市の数が1000になったら、それ以後は新しく加わる人口群は既存の都市に人口に比例した確率で配布される。図を見ればわかるように、(A) においてベキ分布は成り立っているが、(B)においては下の方の順位でベキ分布からグラフが下へと外れている。これも切り捨てベキ分布であることを示している。
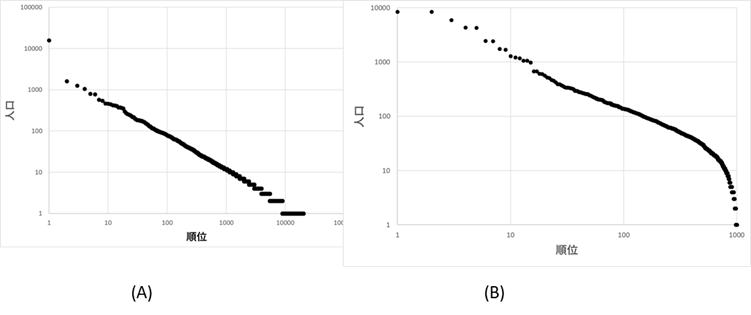
(A)都市の数制限なし、(B)都市の数 1000まで
これ以外でも、ベキ分布のメカニズムに何らかの制限をつけると切り捨てベキ分布が得られるようである。医療における例は3章で再度論じる。前に述べた、ベキ分布生成のモデルは全て理想的な条件である。実際の世界においては、土地面積、人口、社会的な問題による制限がある場合がほとんどである。そのため、完全な形のベキ分布が存在することはまれである。特に医療や社会現象においては制限が必ずあると思われる。そのため、実際の応用を考える時には、このような制限があることを考慮する必要がある。
第3章 医療における複雑性
1.生体におけるカオスとその解析
多数の自由度から成る力学系においてもカオスが発生する。しかも、そのカオスが少数の自由度で決定される。しかし、それらを規定する方程式は見つけられない。生体は多数の要素から成る複雑な系である。しかし、それらが相互作用するときには何らかの秩序が出てきて、それらは少数の自由度で記述できる。そうであるならば、生体の各種の信号系の中にカオスが存在する可能性がある。そのようにして、生体についてのカオス研究が行われている[2]17。
時系列データがカオスであるかどうか、あるいはその分析を行うためにはいくつかの作業が必要である。時系列データ18は一般には1次元のデータである。上記で述べたように、多数の自由度の力学系にある秩序が生まれて少数の自由度で記述できるようになるが、少数であっても多次元である。一次元の時系列データがカオスであるかどうかを判定するためには、まず、時系列データからもとの多次元の相空間上の相図を再現する必要がある。その方法が埋め込みである。1次元データを \(m\) 次元の相空間で表現するには次のように行う。
もとの1次元の時系列データを \(x(k)\) とする。このとき遅れ時間 \(\tau\) を導入して \(m\) 次元の点を次のように定義する。
\begin{eqnarray}
u(k)=\left( x(k), x(k- \tau), x(k-2 \tau), \ldots, x(k-(m-1) \tau) \right) \tag{Ⅲ-3-1}
\end{eqnarray}
これが、観測データに対する元の系の状態に対応する点である。この点を \(m\) 次元の空間に再現することによって、元の力学系の構造を調べることができる。このような方法の正しさを保証しているのがTakensの「埋め込み定理」である。これらの詳細は成書を参照していただきたい[3]。元のデータをこのような \(m\) 次元の相空間に埋め込むことによりアトラクターの形を再現するだけではなく、リアプノフ指数、アトラクターの次元なども計算可能となる[28][29]。
カオスを示す時系列データにはいくつかの特徴がある。その第1はデータのパワースペクトルが連続であるということである。パワースペクトル19というのは簡単に言えば、周波数成分の相対的な大きさである。物理的に言えば電磁波や音波などにおいては各周波数のエネルギー密度ということになる。例えば、正弦波 \(\sin(2\pi ft)\) は、ただ一つの周波数 \(f\) の波から成っている。このような波のパワースペクトルは周波数が一つしかないので、周波数 \(f\) の地点でのみ値がある(図Ⅲ-3-1a)。しかし、一般の音波や電磁波は多数の周波数の波の和から成り立っている。例えば楽器の音はベースの周波数以外に多数の倍音から成り立っている。このような波はパワースペクトルで表すとベースの周波数とその倍音の成分からなるので、飛び飛びの場所に値が出てくる(図Ⅲ-3-1b)。それに比べて、カオスのような時系列データはそのパワースペクトルが飛び飛びではなく連続な成分で表される(図Ⅲ-3-1c)。
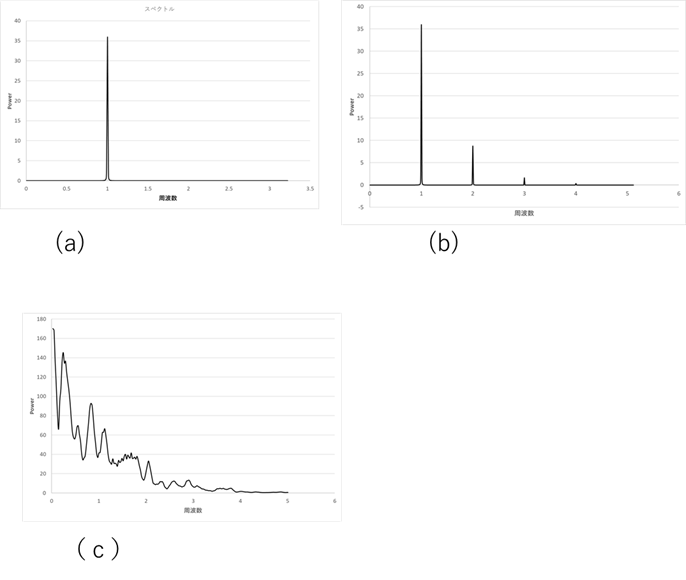
医療におけるパワーススペクトルによる解析は脳波や心拍数(HR)については以前より行われていた[30]。心拍数の時系列データからパワースペクトルを計算し、各周波数成分を計算することにより分析する。周波数成分のうち、0.15~0.40Hzのhigh-frequency band(HF)は副交感神経の活動の影響を強く受け、0.01~0.15Hzのlow-frequency band(LF)は交感神経の影響を強く受けるといわれている。このHFとLFの比較により自律神経系の活動状態の推定を行うことができる。
このような生理的な見方に対して、Goldberger等[31]は別の見方を提示している。正常な状態ではHRは時間的に一定ではなく、つねに揺らいでいる(fluctuate)。このようなときにはHRのパワースペクトルは連続な広がりを示している。しかし、心不全など心臓状態が悪くなると、HRの揺らぎがなくなり、HRは周期的な変動を示したり、一定の値になったりする。このことを、心不全患者や突然死をした患者のHRを調べることによって示した。カオス理論の言葉で述べれば、HRは正常なときにはカオス的変動を示し、危機的な状態になるとHRが周期的あるいは固定されてしまうということを意味している。従来、「生体にはホメオスタシスがあり、体内の環境を一定に保とうとする」という考えが一般的であった。これに対して、Goldbergerは揺らいでいることが正常であり、固定する、あるいは周期運動をすることは異常であると述べたのである。これは、揺らぎというものに初めてポジティブな意味を与えたともいえる。また、同時にカオス現象というものに、生理的な意味を与えたとも考えられる。
カオスを示す時系列データのもう一つの特徴は、そのデータのリアプノフ指数が正であるということである。カオスの特徴のひとつは初期値鋭敏性である。二つの似通った状態から出発しても、時間がたつに従いその状態が大きく異なっていくというのが初期値鋭敏性である。このことを、力学系の言葉でいえば、二つの初期値がどんなに近くにあっても、時間がたつに従って指数関数的に遠ざかるという意味である。すなわち、二つの軌道が \(\exp(\lambda t) (\lambda >0) \) の形で遠ざかる。この遠ざかる割合を決める \(\lambda \) の平均値をリアプノフ指数(Lyapunov exponent、Lyapunov number)と呼んでいる。この \(\lambda\) が負であれば、二つの軌道は近寄っていき、将来的には実質的に同じになる。しかし、\(\lambda \) が正であれば二つの軌道は指数関数的に離れて行ってしまう。このことから、時系列データから \(\lambda \) を求めることができれば[32][16][29]、時系列データの表す系がカオスであるかどうかを決めることができる。
生体の時系列データからリアプノフ指数を求めた代表的なものとして津田、田原、岩永による指尖脈波(finger plethysmogram)による指の血流波形の分析がある[33]。指尖脈波というのは指先の血流の変化を知るために指先に光を当てその変化を記録したものである。血中酸素量を測るパルスオキシメーターにおいても使われている。被検者の指に指尖脈波計を装着することにより指先の血流の変化に対応した波形が得られる。津田等は岩永等によって開発された指尖脈波の測定・計算機器により、指尖脈波のリアプノフ指数を測定して、指尖脈波がカオスであることを証明した。さらに、この波形を4次元の相空間に埋め込むことによりアトラクターを再現した。さらに、田原等[34][35]はこのリアプノフ指数やアトラクターの形が被検者の精神状態によって変化することを見出し臨床に応用可能であることを示した。
津田等の発表以後、多くの生体信号に対してカオス分析がなされている。住田等は瞳孔径の変化がカオスであることを見出している[36]。それ以外にも脳波、心電図などに関してもカオス分析が行われている[37]。それ以後も多くの生体におけるカオスが発見されており、生体においてカオスは普通の現象であると考えられている。田原等はさらに進んで、生体カオスの多くの知見に基づいて、健康の概念を「心身間、および個人・社会間にフイードバックループが形成されることによる関係の自律形成」ととらえている。そして、「健康状態は何らかの形で個人と社会の境界である身体の表面で表現される」という視点に立ち、身体表面に現れる状態を特徴づける指標として「身体言語パラメータ(somato-semantic parameter)」という考えを導入し、活用しようとしている[追加1][追加2][追加3]。そして、生体のカオスのほとんどが、脈波、心音、心電図、脳波、瞳孔径、等々の身体言語パラメータの測定、解析に由来すると述べている。
カオス現象は工学などでも表れてくる、しかし、そのあらわれ方は、対象の制御に関して、制御不可能な現象としてとらえられ、問題は制御においていかにしてカオスを防ぐかという視点が多くみられる。しかし、生体においては、カオス自体が生体にとって大きな利点があるのではないかと考えられている。従来生体においてはホメオスタシスの概念が大きな比重を占めていた。その概念は生体の色々なパラメータが一定に保たれる現象ととらえられていた。しかし、生体におけるカオスの発見に伴い、一定であるという静的な生体概念から、変化しつづける中での安定ということの重要性が認識された。金子、津田、田原等はこのような現象に対してホメオダイナミックス(homeodynamics)という新しい概念を打ち出している。
指尖脈波の臨床への応用も行われつつある[41][42][43]。それらは、精神や行動の問題に対するものが多い。指尖脈波はもともと人間の血流に対する分析である。血流への神経支配は主に交感神経と副交感神経においてなされている。人間の精神はこれらの神経支配を通じで血流に影響すると考えるのが普通である。そうであるならば、神経支配との関連の研究がもっとあってもよいはずであるが、あまり見かけない。そこで、ここでは指尖脈波が開発された当時に予備的調査として行ったデータの分析結果をお示しする。予備的調査であり厳密にコントロールされてはいないため、得られたデータの信頼性については問題があるが参考までに結果を述べる。
ペインクリニック領域に星状神経節ブロック(SGB)という手技がある。これは、人の首の頸椎のそばに注射により局所麻酔薬を注入する手技である。これにより交感神経節の一つである星状神経節を一時的に麻痺させることができる。一時的に交感神経節が働かなくなるために、その神経節の支配領域である顔面、上肢などの血流が改善する。人の上半身の痛み、顔面のベル麻痺、特発性難聴に対する治療の一つとして広く行われているブロックである。

(A)SGB前 リアプノフ数=0.129
(B)SGB後 リアプノフ数=0.445
星状神経節ブロックが交感神経節に対するブロックであるため当然、上肢の血流に影響を与える。そのことは指尖脈波にも影響すると考えられる。そこで、星状神経節ブロックを行う前後での指尖脈波の変化を調べた。同時に全身の自律神経系の影響を見るために、心拍数のフーリエ解析も行った。ただ、心電図を記録していないため指尖脈波の波形の2次微分から心電図のR-R間隔と強く相関するa-a間隔を測定しR-R間隔の代用とした[44]。
星状神経節ブロックの前後において指尖脈波を測定し、4次元にてアトラクターを再構成しリアプノフ指数を求めた。同時に前後の心拍数(実際はa-a間隔の逆数)をフーリエ分析しそのスペクトルの低周波成分LH(0.02~0.15Hz)と高周波成分HF(0.15~0.4Hz)を求め、その比LF/HFを計算した。
図Ⅲ-3-2は星状神経節ブロックの前後での指尖脈波のアトラクターの図である。この例ではSGB後にリアプノフ数が増加しているのが分かる。図Ⅲ-3-3の(A)はSGB後のリアプノフ数からブロック前のリアプノフ数を引いた結果である。図で分かるように、SGBによりアトラクターのリアプノフ数が増加する場合が多いことが分かる。実際、前後のリアプノフ数の差の検定ではp=0.06(両側)という結果であり、有意ではないが、傾向としては星状神経節ブロックによりリアプノフ数が増加する傾向があるとは言える。
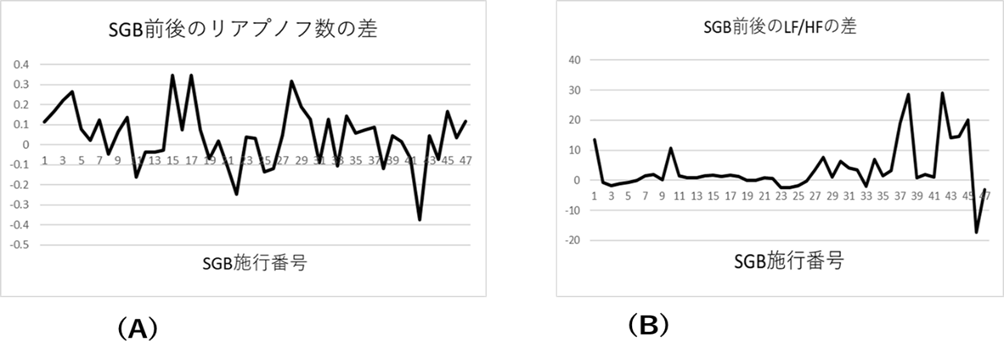
(A)リアプノフ数の変化
(B)LF/HFの変化
同時に測定したブロック前後のLF/HFの差のグラフは図Ⅲ-3-3の(B)で示した。ブロック後にLF/HFが増加しているのが分かる(p=0.003 両側)。心拍数の低周波成分LFは主に交感神経の活動を表し、高周波成分HFは主に副交感神経の活動を表すといわれている。今回の結果から見るとブロックによって交感神経の活動が増すという結果になっている。星状神経節は局所の交感神経節の活動を抑制する。今回の結果は局所の交感神経節のブロックにより全身の交感神経節の活動が増したという結果になっている。ただ、この結果の解釈についてはSGBによる影響、臥床の影響、針を刺すことの影響などを考慮する必要がある。また、すでに述べたように今回のデータはそれほど信頼できるものではないので、断定することはまだ不可能である。リアプノフ数についても、ブロックによってほぼ増加するという結論が得られている。これの解釈は残念ながら今の時点では十分な説明をつけることはできない。
指尖脈波の変化の生理的な意味については今のところはっきりしない。力学系の理論により生体にカオスが発生することは予見できるかもしれないが、その生理的、あるいは生物的な意義についてはまだ、研究が始まったばかりである。生理的な意義を調べるためには力学的理論からだけでは不十分であり、より生理的、医学的な研究が必要である。
最近では、胎児と母の心音を母の声刺激、他人の声刺激、刺激のない状態、等々のさまざまな状態で同時測定し、両者が決定論的カオスであることも示されている[追加4][追加 5]。これは、心音がカオスであると同時に外部刺激の影響で変化することを示している。カオスの環境との相互作用に伴う変化についてはあまり報告が見られないので、今後の発展が期待される。
2.医療における「ベキ分布」
図Ⅲ-3-4(A) はある病院の眼科の病名頻度(ある病名が付いた患者の数)に対するZipfプロットである。横軸は病名を頻度順に並べたときの順位であり、縦軸はその順位の病名の頻度である。実線は \(Y=812/X^{1.04}\ のグラフである。実線のグラフが棒グラフとよく一致しているのがわかる。このことから眼科病名の頻度はだいたい \(Y=812/X^{1.04}\) でよく表されると考えられる。既に2章で述べたように、データのZipfプロットにおいて、順位 \(X\) の頻度 \(Y\) が \(Y=A/X^{\zeta}\) という式で表されるとき、このデータはベキ分布に従う。ベキ分布のベキ指数 \(\alpha\) と \(\zeta\) の関係は \(\alpha = (\zeta + 1)/ \zeta \) となる。この \(\zeta\) は、すでに2章で述べたように、ベキ分布に従うデータのZipfプロットは両対数グラフで表したときに直線となり、その直線の傾きから求めることができる。図Ⅲ-3-4(B)は(A)で示した眼科の病名頻度の両対数グラフである。グラフがよく直線にフィットしており、眼科病名がベキ分布に従うことがわかる。この直線の傾きから眼科病名分布の \(\zeta\) は1.04であることがわかる。また、ベキ指数 \(\alpha = (\zeta +1)/ \zeta =1.96\) となる。以上のように眼科の病名頻度はほぼベキ分布に従うことが分かった20。実は病名の分布は眼科に限らずベキ分布に近い分布に従うことが分かっている[48][49]。病名頻度分布については第4章で改めて論ずる。
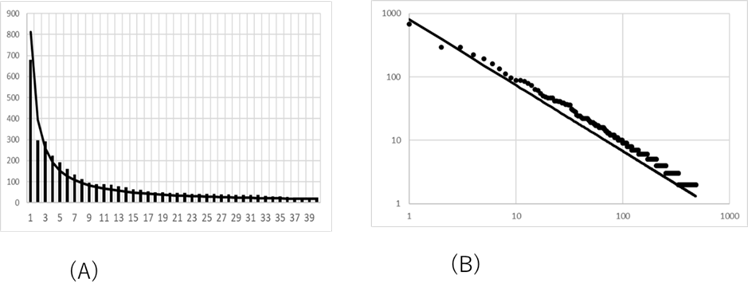
(A)病名頻度
(B)病名頻度の両対数グラフ
図Ⅲ-3-5、図Ⅲ-3-6はある急性期あるいは慢性期の病院の入院日数の分布である。入院日数2、3日にピークがありその後、急激に減少するが、ゼロにはならないでいつまでも裾を引きながらゆっくり漸減していく。この分布もすそ野の長い分布である。両対数グラフは回帰直線に比べて少し上に凸のグラフをなっており、対数正規や切り捨てベキ分布に近い分布である。その発生メカニズムについては3章-4において改めて述べる。このような長いすそ野のために、平均入院日数21よりも長い入院日数の患者が沢山いるのが特徴である。急性期と慢性期では平均入院日数は大きく異なるがどちらもすそ野の長い分布を示すことは興味深い。後述する発生メカニズムは「ドリフト付きのランダムウォークモデル」である。急性期と慢性期の違いは主にこのドリフトの大きさの違いと考えられる。ドリフトの大きさの違いが平均入院日数の違いに現れ、ランダムウォークメカニズムが長いすそ野を引かせていると思われる。いずれにしろ、長いすそ野の分布であるために、入院日数の予想は非常に難しく、入院管理を難しくしている。
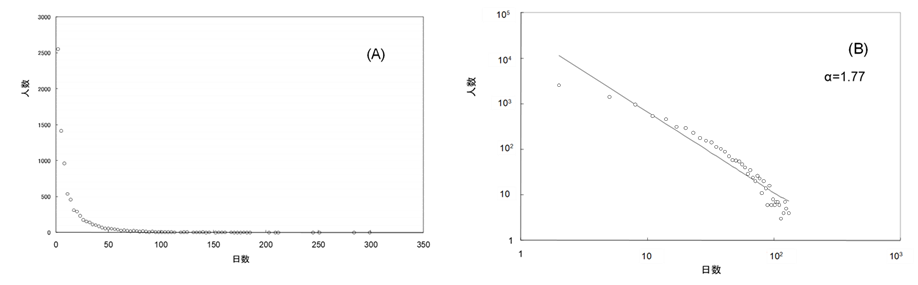
平均在院日数=15日
(A)入院日数分布、(B)入院日数分布の両対数グラフ \(\alpha =1.77\)

\(\alpha=1.24\) 平均在院日数=148日
病名分布においてベキ指数 \(\alpha\) は2(\(\zeta\) では1)前後であり、入院日数分布では図に示しているように、ベキ指数は急性期病院で1.77、療養型病院で1.24である。ベキ指数が2以下を示すことは重大な意味を含んでいるが、それについては以下の節で述べる。
筆者が調べたところでは、医療においてベキ分布あるいは「すそ野の長い分布」はそれほど珍しくはない。表Ⅲ-3-1にすそ野の長い分布を示す医療における事象を示した。表で「?」の付いているものは十分なデータが無いために推定のみの事象である。しかし、手術時の大出血が時々見られることや、多くの病院で手術時間の管理がうまくいかないことを考えると、これらの分布が「ベキ分布」もしくは「すそ野の長い分布」であることは十分推測される。

3.すそ野の長い分布の医療への影響
3-1 異常値は稀ではない
医療においてしばしば見られるベキ分布などの「すそ野の長い分布」は正規分布に慣れた人から見ると非常に不思議な特徴を有している。それらの性質を1)異常値は稀ではない、2)平均値が役立たない、の二つに分けて説明する。以下の説明は純粋な「ベキ分布」として述べる。一般の「すそ野の長い分布」に関しては、無限などの言葉を「非常に大きな値」と読み変えて理解していただきたい。
まず、異常値は稀ではない、もしくは「稀なことがしばしば起こる」と表現できる事実である。このことを病名頻度分布を例にして述べてみる。
図Ⅲ-3-7 (A) はある病院の内科病名の頻度分布である。異常値とはこの図では〇をつけたすそ野の部分のことである。このすそ野が非常に長い(ロングテール)のがベキ分布の特徴である。図Ⅲ-3-7 (B) はベキ分布と正規分布を重ねて描いたグラフである。正規分布は左右対称の右側半分のみを示している。図からわかるように「ベキ分布は \(x\) (横軸)の小さい部分では急激に減少するが \(x\) が大きくなると正規分布に比べてゆっくり減少する。そのため、正規分布ではほとんどゼロになるようなすそ野でも正の値で長く裾を引くのである。
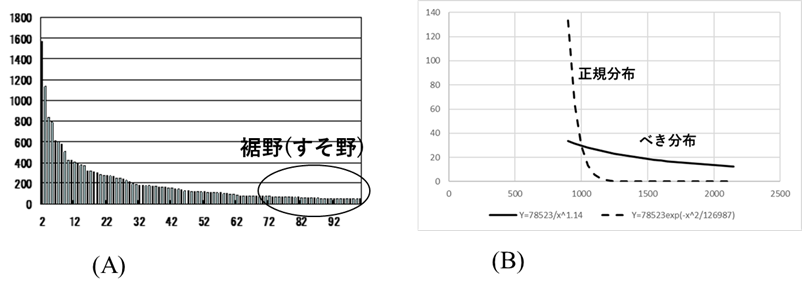
このことの影響を病名付けを例にして考えてみる。図Ⅲ-3-8は図Ⅲ-3-7 (A) の病名の頻度分布を累積割合の形に書き直したものである。すなわち、順位 \(x\) でのグラフの値は図Ⅲ-3-7 (A)での1から \(x\) までの順位の頻度を全部足したものである。言いかえると、順位 \(x\) での値は順位1から \(x\) までのすべての病名で病名付けできる患者の総数を表している(ただし、グラフでは全患者数に対する割合で表している)。
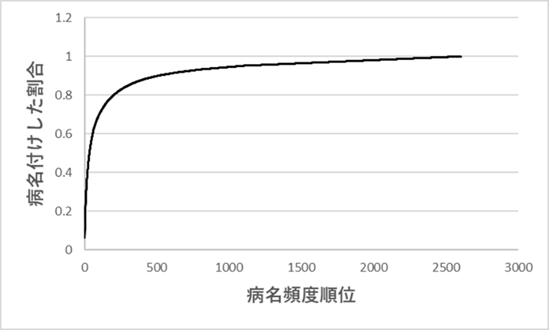
この図を見るとわかるように、約100個の病名で全患者(このデータでは数万人)の約70%の患者に病名をつけることができる。この数字を見たときには、「全員に病名を付けるには病名が数百個もあればよいだろう」と思わないであろうか。しかし、グラフを見るとこの予想が外れるのがわかる。病名数500で9割の患者に病名付けができる。千では9.5割、その後、グラフの増加はだんだんゆるくなっていく。結局、このデータではすべての患者に病名を付けるには数千個の病名が必要である。全員に病名を付けるのは最初の予想に反してかなり大変である。
病院オーダエントリシステムあるいは電子カルテ内に病名オーダというオーダリングがある。これは、患者を診察するたびに医師が患者の病名をコンピュータに入力するためのオーダである。入力された病名は医事システムなどに取り込まれレセプトなどに利用される。病名を自由表記で入力すれば後のデータ利用において不便であるため病名コードでの保存が必要である。そのため、かつては病院ごとに病名マスターを作っていた22。このマスターを作成するとき次のように行うとしよう。最初にいくつかの病名を用意する(数千個)。その時点で運用を開始すれば足りない病名が出てくるので毎年その病名をマスターに追加する。この作業を毎年繰り返す。この際の期待としては、「毎年この作業を繰り返せば追加する病名は減っていき、何年かすれば病名の追加はほとんどいらないであろう」というものである。しかし、実際に起こったことは次のようなことである。
- 1)病名マスターには毎年、同じ数だけ病名を追加しなければならない。
- 2)追加した病名の多くが二度と使われない。
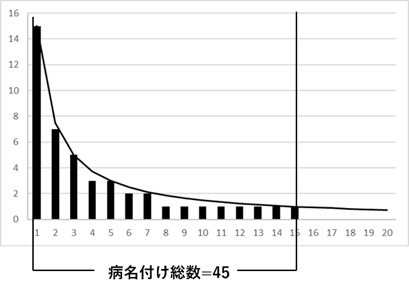
このような現象は病名頻度の分布がベキ分布であるとすれば説明できる[50][51]。図Ⅲ-3-9は \(Y=A/X\) のベキ分布のグラフを示している(図では \(A=15\) )。\(A/X\) のグラフは \(X\) を変化させたとき、一般に小数点を持つ値になる。実際の病名頻度は小数点のない整数である。そのため、グラフに示すように、実際の頻度は \(A/X\) の値の少数点以下を切り捨てた棒グラフの値になる。又、当然頻度は1以上でなければならないので、\(A/X \lt 1\) の範囲は意味を持たない。結局、このグラフで意味を持つのは、\(X\) が1から15までの範囲である。この範囲の病名頻度を足しあわせると45となる。これは、病名頻度が \(15/X\) のグラフに従うとすれば、15種類の病名で45人の患者に病名を付けることが出来るという意味になる。同様にして \(A\) を30にすると、30種類の病名で111人に病名を付けることが出来る。言い換えれば、111人に病名を付けるには40種類の病名が必要である。このように、病名頻度分布を使えば、病名付けに必要な病名数が推定できる。そこで、\(A\) をどんどん大きくしたとき必要病名がどのように変化するかを調べた。
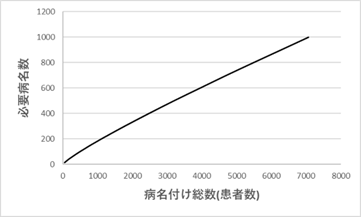
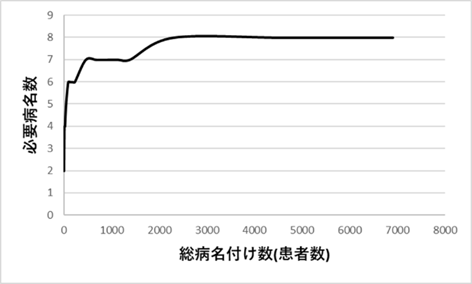
図Ⅲ-3-10はそのようにして調べた必要病名数をあらわす。横軸は病名付けが必要な患者数である。それらの患者に病名を付けるとするとどれだけの病名が必要かを縦軸に示している。このグラフを見ればわかるように、患者数の増加に伴って必要病名数がいつまでも増加していく。必要病名数は病名付けする患者数の増加に伴い無限に増加するのである。
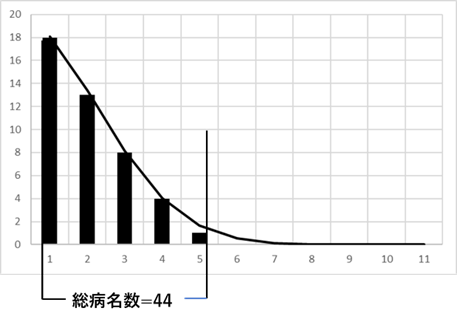
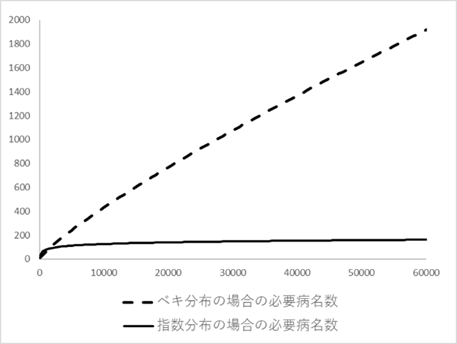
同じことを病名頻度分布が正規分布をするとした場合の計算をしておこう。図Ⅲ-3-11は病名頻度が正規分布をするとした場合の模式図である(正規分布の右半分を使っている)。前と同様の考えで、総病名数に対する必要病名数が計算できる。図では総病名数44に対して必要病名数が5であることがわかる。ここで、病名分布が同じであるとした場合の、総病名数に対する必要病名数をプロットしたものが図Ⅲ-3-12である。この図からわかるように総病名数が増加しても必要病名数はある一定値以上には増加しない。このような分布であれば、前もってある数の病名を用意しておけば、それに含まれない病名は非常に例外的であり無視したり、除外することも可能である23。図Ⅲ-3-13には、病名頻度がベキ分布をするとした場合と指数分布をするとした場合について、必要病名数の変化を計算した結果を示している。指数分布でも正規分布と同様に必要病名数はある一定値以上には増加しない。このように、必要病名がどんどん増えていくのはベキ分布のすそ野(異常値)が正規分布などに比べて長く、異常値が稀ではないためである。経験で得られる「追加した病名の多くが二度と使われることがない」という感覚はまさにこのことを表している。
「異常値が稀ではない」という感覚は他の臨床経験でも得られる。手術に際して稀に予測できなきないほどの大出血が起こるが、この現象は手術に携わる多くの医療者が経験することである。そのほかにも時々異常に長い手術時間が起こること、クリティカルパスにおけるバリアンスが減らない事実なども、「異常値が稀ではない」という現象であると思われる。
3-2 平均値が存在しない
二番目の特徴である「平均値が存在しない」という現象を入院期間の分布を例にして説明する。入院日数の分布がベキ分布に近いすそ野の長い分布をすることはすでに述べた。そこで、ベキ分布であるとした場合に何が起こるかを考える。分布から平均入院日数が計算できるが、すぐに分かるようにベキ指数 \(\alpha\) が2以下ならば平均値は発散(無限)する。またベキ指数が3以下なら分散が発散する24。このように、ベキ指数が2以下の場合には入院日数の平均値も分散も発散してしまう。数学的にはこれだけの話であるが、実感として入院日数が発散するということはどのように解釈すればよいのであろうか。この点について以下に説明する。
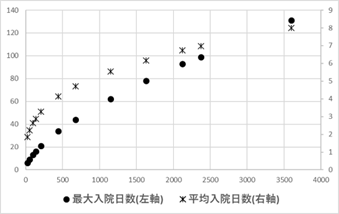
今、45人の入院患者があり、その入院日数の分布が \(A/X\) に従うとしよう。この場合、平均入院日数を計算することは可能である。この場合の入院日数の分布は \(A=15\) とすると、図Ⅲ-3-9と同様になる25。この場合、平均入院日数=(15(人)×1(日)+7×2+5×3+…+1×15)/45(人)=4.2(日)となる。同様にして \(A=30\) とすれば入院患者数が111人になり、平均入院日数は6.86日と計算できる。ここで注目すべき点は平均入院日数が4.2から6.86日へと増加している点である。入院患者数が増えていったときの平均入院日数を同様の方法で計算した結果が図Ⅲ-3-14である。図は入院患者の数と平均入院日数、最長入院日数の関係を表している。図を見れば明らかなように、患者数が増えるに従って平均入院日数も最長入院日数も増加している。この増加はいつまでも止まらない。患者数が増えればどこまでも平均入院日数が増えていく。これが、平均入院日数が発散(無限)するという意味である。
ちなみに、図Ⅲ-3-15は入院日数の分布が指数分布26をしているとした場合の平均入院日数の変化を表しているが、この場合は患者数が増加しても平均入院日数は一定の値に留まっている。正規分布でも同様である。
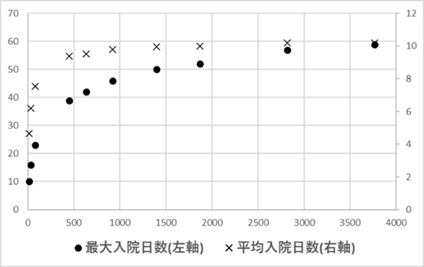
このように、平均入院日数が発散するということの実際的な意味は「考える患者数が増える(観察時間が増える)に従って平均値が大きくなっていく」ということである。当然、このように集団のサイズによって変化してしまう平均値は集団の指標としては使えないであろう。
ついで分散の発散についてであるが、これはデータのばらつきが大きくなるということである。たとえ平均値が有ったとしても(\(2 \lt \alpha \leqq 3\))、患者毎の入院日数のばらつきが大きすぎてやはり平均入院日数を集団の指標として使うことは不可能になるであろう27。無理に指標とするには異常値を捨てる必要がある。例えば、長期入院患者を退院させるなどの処置を行うことが必要になってくる。現在、病院には入院日数を短くする圧力がかかっている。そのため、実際に長期入院患者に対する退院勧告などが行われるようになっていると聞くが、これはベキ分布の性質から考えると当然起こりうることであるとも言える。
入院日数がベキ分布をするのかどうかは、医療経済学的には非常に重要な問題である。近年、医療マネージメントツールとしてDRG(Diagnosis Related Group)という患者分類方法が発達してきている[52]。DRGとは入院患者の分類法である。入院患者を病名その他の指標により500程度に分類する。この分類法は、「同じ分類に含まれる患者は、入院日数、医療材料、人的資源など患者に要する医療資源の使用量が似通っている」という性質に基づいている。医療資源の使用量は、治療に要する費用に関係する。患者をDRGに分類することにより、入院中の医療資源の使用量や費用を前もって予測することが可能となる。この性質を使って、DRG毎の医療費の定額払い制度(DRG/PPS: Diagnosis Related Group – Prospective Payment System)、病院の質と費用の管理などに利用されている。
しかし、このような分類が可能であるためには、資源使用量の分布が正規分布あるいは少なくとも有限の分散をもつことが必要である。もし、この仮定そのものが成り立たないならば、DRG分類やそれを応用した分類、例えばDPC(Diagnosis Procedure Combination)などの方法そのものが成り立たない。この結果は重大である。入院日数は入院患者の重要な医療資源のひとつである。2以下のベキ指数を持つベキ分布は分散のみならず平均も発散してしまう。このことは、DRGという分類の前提そのものが崩れてしまう可能性を示している。実際には入院日数は厳密な意味ではベキ分布ではない。ベキ分布に比べればすそ野が短い(2章参照)。しかし、平均値や分散が大きいことに変わりないので、ここで述べたような解釈はそれほど間違ってはいないだろう。
4.医療におけるベキ分布の成因
4-1 医療における三種類のベキ分布
前節で見たように、ベキ分布は医療に多大な影響を与える。医療政策、医療マネージメントを考える場合に医療に存在するベキ分布あるいは「すそ野の長い分布」の問題を避けて通ることはできない。医療においてなぜベキ分布が起きているかを調べることは、単に興味の問題だけではない。メカニズムがわかるならば、そのようなベキ分布に対するコントロール可能性、対処可能性を知ることも可能になるであろう。
物理現象を含めての一般的なベキ分布の成因については第2章において既に述べた。ここでは、医療におけるベキ分布の成因を考えるのに参考になると思われる理論を簡単に述べておく。医療において見られるベキ分布は大きく三種類に分類できる。一つ目は病名の頻度や手術術式の頻度のようなカテゴリーの頻度分布である。二つ目は手術中の出血量の分布のような量の分布である。そして、三番目が入院日数、手術時間、病気の回復までの期間のような時間分布に関するものである。これらの性質はかなり異なり、可能性のあるメカニズムも異なっていると考えられる。病名頻度の分布については、第4章にて改めて論じるので、ここでは、入院日数分布と手術中の出血量の分布について考える。
4-2 入院日数分布
すでに、3章-2で述べたように、入院日数分布はすそ野の長い分布をする。一般には対数正規分布をするといわれているようである[24]。図Ⅲ-3-5からわかるように、両対数グラフは回帰直線に比べて少し上に凸のグラフになっている。このことから、入院日数分布は対数正規分布ではないかといわれている[53](3章-2参照)。ただ、その成因についてははっきりしない。
入院日数の分析は広い意味での生存時間分析に含まれる[25]。医学においては、治療の効果を見るために治療を行った群と行わなかった群で生存時間に差があるかどうかの検定などに使われる。その際、仮定される生存時間分布としては指数分布、対数ロジスティック分布、対数正規分布、逆ガウス分布などがある。入院日数に関しては、データと、それらの分布との比較によって、対数正規分布と逆ガウス分布が最適なモデルであると言われている[54]。Whitmoreは、正のdrift項つき1次元ランダムウォークモデルによって入院日数が逆ガウス分布に従うことを示している[55]。
Drift項付きのモデルの前に、まずランダムウォークモデルを考えてみよう。このモデルでは患者の日々の健康状態を1つの整数 \(S\) で表す。入院時の健康状態を0として、日々ランダムに+1もしくは-1だけ変化する。健康状態 \(S\) がある値 \(z\) (\(\gt 0\))に初めてなった日に退院であるとする。形式的にモデルを表現すれば次の様になる。
入院日数のランダムウォークモデル
日時 \(n\) での患者の状態として状態の変数 \(S(n)\) を考える。
患者は入院時には状態0であるとする。退院決定は状態がz(>0)となったときとする。各時点で状態は改善(+1)か悪化(-1)だけで、ランダムに変化する。すなわち、
\begin{eqnarray}
S(n+1)=S(n)+X_n \tag{Ⅲ-3-2}\\ \\
X_n=
\left\{
\begin{array}{l}
+1 確率 p\\
-1 確率 q=1-p
\end{array}
\right.
\end{eqnarray}
\(S(n)=z\) となった時点 \(n\) を入院日数とする。
以上の単純なモデルの場合、入院日数が \(n\) となる確率 \(w_{z, n}\) は理論的に計算でき、次のようになる[20]。
\begin{eqnarray}
w_{z, n}=\frac{z}{n}
\begin{pmatrix}
n \\ \frac{1}{2}(n-z)
\end{pmatrix}
p^{\frac{1}{2}(n-z)}q^{\frac{1}{2}(n+z)} ただし、
\begin{pmatrix}
n \\ x
\end{pmatrix}
は二項係数 \tag{Ⅲ-3-3}
\end{eqnarray}
\(p \neq q\) の場合は \(n\) が大きいところでは漸近的に次のようになる28。
\begin{eqnarray}
w_{z, n} \approx C \left ( \frac{n-z}{2} \right )^{-\frac{3}{2}}b^{-(\frac{n-z}{2})} C=\frac{z(2q)^z}{2\sqrt{\pi}}
b=\frac{1}{4pq} \gt 1 \tag{Ⅲ-3-4}
\end{eqnarray}
式Ⅲ-3-4は指数分布とベキ分布を混合したような分布で、\(n\) が比較的小さいところでは、ベキ分布様の振る舞いを示し、\(n\) が大きい領域では指数分布に近い振る舞いを示す。すなわち、これ自体が2章で述べた「切り捨てベキ分布」の形になっている。よって、このモデルを入院日数モデルの一つと考えることも可能である。しかし、入院日数を「切り捨てベキ分布」として考察した論文は見られない。
\(p=q\) の場合の漸近分布は次のようになる。
\begin{eqnarray}
w_{z, n} \approx \frac{z}{2\sqrt{\pi}} \left(\frac{n-z}{2} \right)^{-\frac{3}{2}} \tag{Ⅲ-3-5}
\end{eqnarray}
これは、分布が指数1.5のベキ分布である。この指数1.5という数字は興味深い。入院分布の実際のデータによれば[56]、指数が1から2の間に収まっているものが多い。このことは、このモデルにある程度正当性があることを示している。しかし、このモデルを少し変形するとWhitmoreのdrift項つき1次元ランダムウォークモデルが得られる[55][24]。
そのモデルは上記のランダムウィークモデルに正のdrift項をつけるだけで得られる。要するに、治療などによって、患者の状態が一定の速度で改善するという考えである。モデルとしては式Ⅲ-3-2に一定の正の定数 \(\gamma \) (正の整数)をつけるだけである。すなわち
\begin{eqnarray}
S(n+1)=S(n)+X_n+\gamma \tag{Ⅲ-3-6}
\end{eqnarray}
もし、ランダムの項 \(X_n\) が無ければ、入院日数は必ず \( \displaystyle\frac{z}{\gamma}\) となる。状態のランダムな変動によって入院日数が変動するというモデルである。このモデルによる分布は逆ガウス分布となる。
逆ガウス分布というのは、入院日数を \(x\) (実数)とすると、その確率密度は上記の \(z, \gamma \) を用いて
\begin{eqnarray}
p(x)=\frac{z \cdot \exp{(z \gamma)}}{\sqrt{2\pi}}x^{-\frac{3}{2}} \exp{\left(-\frac{1}{2}(\gamma ^{2}x+\frac{z^2}{x})\right)} \tag{Ⅲ-3-7}
\end{eqnarray}
と表される。平均値は \(\frac{z}{\gamma}\) となる。図Ⅲ-3-16に逆ガウス分布の密度関数を示す。両対数グラフで上に凸のグラフで、すそ野の大きいところで直線から下にずれていく。
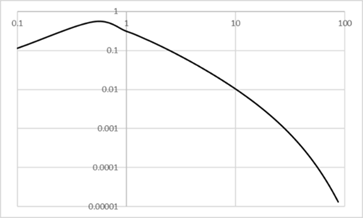
\(z=1 \quad \gamma =0.3\)
グラフはピークが過ぎたところからベキ分布の様に低下するが、上に凸である。
すでに述べた3つのすそ野の長い分布すなわち対数ロジスティック分布、対数正規分布、逆ガウス分布はよく似た形をしており、実際のデータからこの3つを区別するのは難しい。利用する目的や利便性によってどの分布を採用するかは異なってくるようである。ただ、どの分布が正しいかを判定する基準として、その分布が出現するモデルの妥当性も考慮に入れる必要がある。
入院日数の分布は病院の種類によって異なっている。日本においては、病院は急性期、療養型、介護型などに分かれている。これらの入院日数分布はいずれも「すそ野の長い分布」である。それらを、ベキ分布で近似した時のベキ指数はいずれも1~2の間である。入院日数分布をベキ分布でモデル化すると、全ての病院が一つのベキ指数で表現されることになる。しかし、胡内らの論文でも示されているように、病院の種類によって平均入院期間は大きく異なっている[56]。全ての病院が一つのベキ指数で表されるベキ分布に従うとすると、患者数が多くなるとすべて同じ分布関数になるはずである。しかし、データからそのようなことはあり得ないのが分かる。このことは、入院日数をベキ指数という一つだけのパラメータで表すことは不可能であることを示している。上記で説明したベキ分布以外の「すそ野の長い分布」はすべて、複数のパラメータを持っている。複数のパラメータを持てば、パラメータの違いで病院の種類の違いを表現することができる。この点からも、入院日数を完全なベキ分布であると言うのは少し無理があると思われる。
4-3 手術中の出血量
図Ⅲ-3-17はある病院での手術中の出血量データから作成したものである。出血量頻度の両対数グラフ(B) を見ると大体直線性が得られる。このことから、出血量頻度もベキ分布のように見える。ただし、出血量の大きいところで頻度のグラフは直線から下の方へずれているのがわかる。また、データは示さないが、出血量の分布は手術の種類によって大きく異なる。甲状腺の手術など小さな手術では出血量は普通数十から100ml程度である。それに対して胃の手術などは数百ml程度、食道がんや、肝臓の手術になると数リットルも稀ではない。もし、出血量が全て一つのベキ分布で表現できるとすると、たとえ甲状腺の手術であっても何千回も手術をすると、数リットルの出血が起こりうることになる。実際の経験からそれはほとんどあり得ない。このことを考えると、出血量を1つのベキ分布で説明するのは難しいと考えられる。手術の種類ごと別々の分布であり、しかも、出血量の多いところで「切り捨てベキ分布」のような急激な頻度の低下が必要である。
ところで、出血源である血管というのは非常に複雑に枝分かれした形態をしている。このような形態は単純な幾何学では表現できない。このような形態の表現法として近年、フラクタル幾何学という方法が開発されてきている[4][5]。実際、血管系はフラクタルであるという論文は多数発表されている[57][64][59][60][61]。そして、このようなフラクタルである流れの流量に対して高安がモデルを作成している[62]。
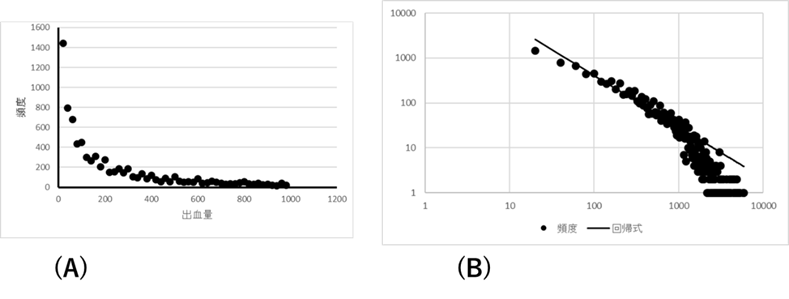
(A)出血量の頻度分布
(B)両対数グラフ 出血量の大きいところで直線から下へずれる
高安のモデルは次のようなものである。
一次元の格子に置かれた整数質量の粒子がある。離散時間でこの粒子がランダムウォークをして凝集する。形式的には次の様に定義される。
- ① すべての格子のsiteに粒子がある。
- ② それらは各時点で、確率0.5で右のsiteに飛び、確率0.5で元のsiteに留まる。
- ③ 飛んだあと、二つ以上の粒子がぶつかれば、それらが一緒になって大きな粒子になる。
- ➃ その後、全てのsitesに単位粒子が追加される。(そのsiteに大きさ \(n\) の粒子があれば、\(n+1\) になる)。以下、②から③を繰り返す(図Ⅲ-3-18)
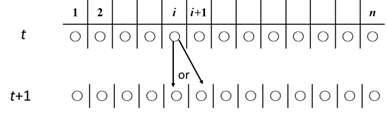
時刻tで \(i\) にある粒子は次の時刻 \(t+1\) で \(i\) に留まるか \(i+1\) へ移る。
\(i+1\) に移った粒子はもともと \(i+1\) にある粒子と合併して質量が増える。
このモデルで、十分長い時間が過ぎた後では、各siteの粒子の質量 \(s\) はベキ分布をする。すなわち相補累積分布関数(CCDF)で表すと \(P(s \geq x) \propto 1/x^{\beta}\) となる。ここで \(\beta\) は0.331程度である。普通の確率密度関数の場合のベキ指数 \(\alpha \) の場合は \(\alpha = \beta +1\) となるので \(\alpha \) は1.331程度となる。左右に飛ぶ確率を色々変えると、\(\beta = \alpha -1 \simeq 1/3 \sim 1/2\) の間で変化する。
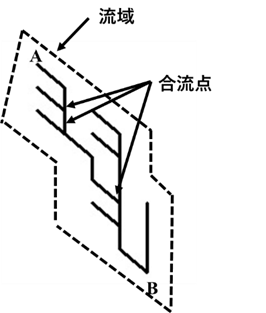
このモデルは見方を変えると、川の流れの各地点での流量の分布という考えに行きつく。1次元のsiteを2次元平面の格子点と考える。各格子点を時間1の流量で水が噴き出している水源と考える。ある点 \((x, y)\) を考える。この点から流れが起こる。この流れは次の時点 \((t+1)\) で左右のどちらかの点、すなわち \((x, y+1)\) か、\((x+1,y+1)\) に流れるとする29。新しい点で、他の流れと合流すれば、二つの流量を合わせ、さらにその地点の噴出し水を合わせた流量となる。合流が無ければ、そこからの噴出し水を流れに取り込む。どこからも川が流れ込まない点では \(t+1\) の時点で新たな流れが起こると考える。こうして、流れの図を描くことができる。
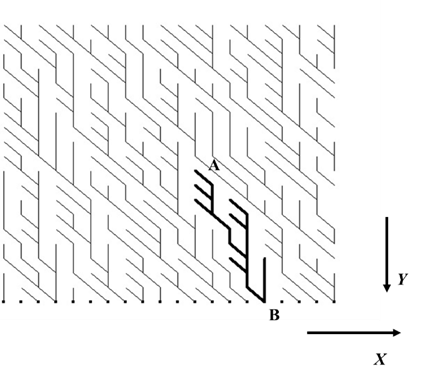
参考文献[66]の図を著者が改変
例えば、図Ⅲ-3-19における流れの開始点AからBまでは、Bへ流れ込む川の図であるとも見える。この部分を書き直したものが、図Ⅲ-3-20である。この図では、川のまわりを点線で囲んでいる。この部分がこの川の流域であると考えられる。
参考文献[62]の図を著者が改変
この図は別の見方をすれば、多数の支流が合流しながら流れていると見ることができる。高安のモデルでの質量とは川の言葉でいえば、川のある点での流量である。支流が二つ合流するとその合流点での流量はそれぞれの支流の流量の和である。結局、ある点での流量はその地点から上流のすべての支流の流量の和である。これは、ある点から上流の流域の面積(正確にはその流域で噴出する水のすべての和)に等しい。図でいえば、B点での流量は図における流域の面積に比例する。この流量が「ベキ分布」をするというのがこのモデルの結果の解釈である。流域の面積というのは河川の幾何学的性質に依存する。高安のモデルは「河川がフラクタル図形で表されるならば、その流域の面積はベキ分布に従う」と言い換えることもできる。
高安の理論は、河川としては単純な形である。この理論は、Rodríguez-Iturbe等によってより複雑な実際の河川に適用されている[63]。その理論の結論を簡単に述べよう。図Ⅲ-3-21は大阪府の河川図の一部の概略図である。この川のように複雑に枝別れしている図は一般にフラクタルと呼ばれている。詳細は参考文献[4][5]を参照してほしいが、フラクタルとは図形の次元が小数点になるような図である。従来の幾何学的な図形は整数の次元を持っている。直線や曲線は1次元であり、普通の平面図形は2次元、立体図形は普通3次元である。しかし、自然にある山並みの稜線の様に複雑に曲がりくねった線は普通1より大きく2より小さい小数点で表される次元を持っている。自然界にある雲の形、河川のかたち、海岸線などはフラクタル図形であるといわれている。カオスにおけるアトラクターも図形としてはフラクタルである。
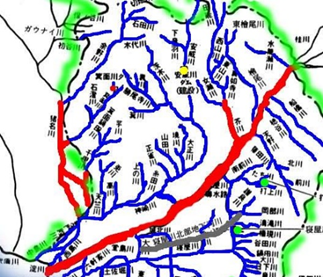
大阪府 都市整備部 河川室河川環境課 管理グループ作成
大阪府のホームページより引用
Rodríguez-Iturbeらは、高安の理論を拡張して、河川のフラクタル次元と高安の理論におけるベキ指数の関係を導いている。彼らは実際の河川図と理論的な考察により次のような結論を得ている。
- (1)実際の河川もフラクタルと考えられる。
- (2)実際の河川の写真から川のフラクタル次元Dを推定できる。
- (3)このDと流量分布の(CCDFの)ベキ指数 \(\beta\) との間には \(\beta \simeq 0.5/D\) の関係がある。
彼らの使った河の写真から得られたフラクタル次元は \(D \simeq 1.1\) であった。結局 \(\beta \simeq 0.5/D \simeq 0.4545\) \((\alpha \simeq 1.4545)\)となり、実測値(0.43)とよく一致した。
河川がフラクタルであるならば、血管系もフラクタルであろうと思うことは当然である。実際、多くの論文で生体におけるフラクタル構造が論じられている[57][64][59][60][61]。その中には血管のフラクタル性も論じられている。血管系がフラクタルであるとすれば、血流に対して高安の理論が適応できるだろう。出血は血管の破たんであるので、破たんした場所の流量に比例するであろう。そのため、高安の理論で出血量の分布を考えることができる。ただ、出血量に応用する場合には、高安の理論での格子サイズについての考察が必要である。高安の理論でははっきり述べられていないが、格子サイズは無限であるという暗黙の了解がある。格子サイズが無限である場合には血流の分布は完全なベキ分布を示す。しかし、格子サイズが有限の場合には、2章で述べた「切り捨てベキ分布」が起こる。実際、高安モデルにおいて格子サイズを有限であるとして、シミュレーションするとその頻度はベキ分布に比べてすそ野においてベキ分布より早くゼロに近づくことが分かる(図Ⅲ-3-22)。
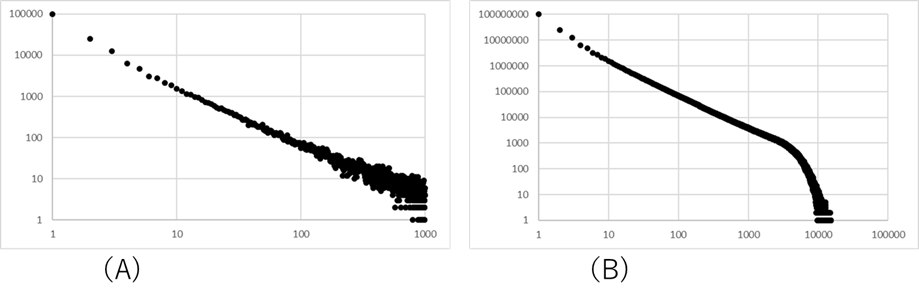
(A)シミュレーション回数 \(2 \times 10^5\) 回 ベキ分布となっている
(B)シミュレーション回数 \(2 \times 10^7\) 回 切り捨てベキ分布である
図からわかるように、格子サイズを有限にすることにより分布はベキ分布に比べて大きい部分で急減に低下する切り捨てベキ分布になることが分かる。このことは、実際の出血分布がベキ分布に比べて上に凸であることとも整合する。さらに、格子サイズを変えると、ベキ分布から外れる点の出血量が異なってくる。そのため、手術の種類により別々の分布が得られる可能性が示される。格子サイズを大きくすれば、大きな手術の出血モデルとなる。格子の大きさを手術の大きさに対応させることによって、手術種類の違いによる出血分布の違いを説明することが可能であろう。
第4章 医療の複雑性の本質
1.病名分布
すでに、第3章-2で述べたように病名頻度分布はZipfの法則を満たしている。それについて、もう少し詳しく述べてみる。すでに、いくつかの研究で病名分布が調べられている[48][49]。いずれの研究においても、病名の頻度分布はZipfの法則を満たしている。
図Ⅲ-4-1(A)はある急性期の総合病院における内科の診断名のZipfプロットのグラフである。診断名を頻度順に並べた場合、x軸に順位、y軸にその頻度をプロットしたものである。図は両対数グラフで表示してある。図を見ればわかるように、グラフがすそ野では直線に良く乗っているのが分かる。すなわち、病名分布がZipf の法則 (ベキ分布)に従っているのが分かる。図Ⅲ-4-1(B)は眼科でのZipfプロットである。こちらも同様にベキ分布に従うことが分かる。しかも、こちらの方が直線への乗りがよいのが分かる。
図Ⅲ-4-1の(A)、(B)は病名を日本語で表記した場合のZipfプロットである。それに対し、(C)、(D)は同じ病院の診断名をICD-1030でコーディングした場合の頻度分布を表している31[56]。こちらもよく直線に乗っているのが分かる。内科、眼科いずれにおいてもICDコードの場合には日本語表記の場合に比べグラフの傾きが大きくなり、順位の小さいところで、直線からのずれが大きくなる傾向がみられる。
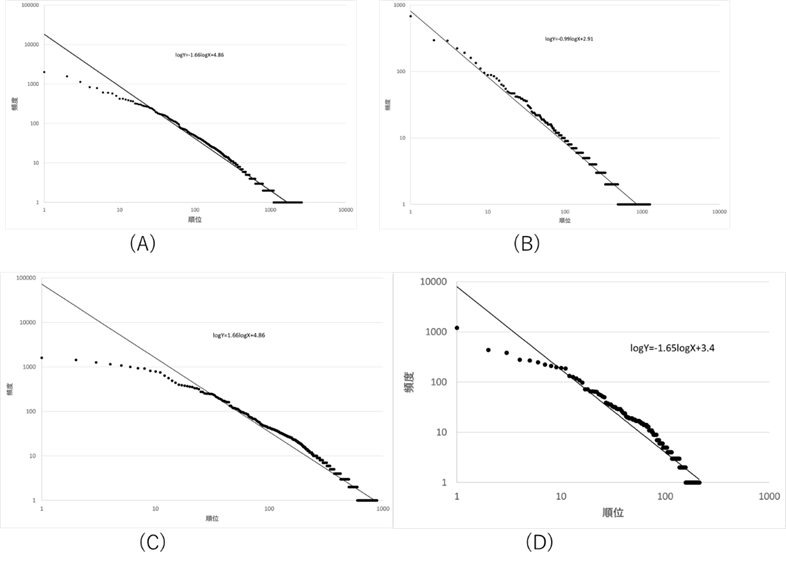
A:内科の日本語表記病名頻度のZipfプロット
B:眼科の日本語表記病名頻度のZipfプロット
C:内科ICD-10コード頻度のZipfプロット
D:眼科ICD-10コード頻度のZipfプロット
それ以外の科においても頻度分布を調べたが、すべて両対数グラフの直線へのフィットは良好である。ただ、順位の高い部分において、回帰直線からずれる傾向がみられる。表Ⅲ-3-1は各科の日本語表記病名頻度とICD-10 コードの頻度分布の要約である。すべての科においてZipfプロットは回帰直線によく乗っている。日本語表記病名の頻度に関しては、そのZipf指数ζは全ての科において、1前後である。ICDコードにおける場合には、日本語病名の場合に比べてZipf指数が大きくなる傾向がみられる。各科毎以外にも、各医師毎についても調べたが、いずれもZipfの法則を満たしていた32。

各医師が診断した病名の集合を、科全体で集めると診療科毎に集計した病名集合に等しくなる。また、診療科毎に集計した病名を全部集めると病院の総病名集合になる。これらがすべてZipfの法則に従うことは、2つのZipfの法則に従う集合(これを、Zipf集合と呼ぼう)を合併(union)すると再びZipf集合ができることを示唆する。このことを簡単な例で示そう。
まったく共通の病名が無い同じ大きさの2つの集合が有り、それぞれがZipfの法則(Zipf指数=1とする)に従うとする(例えば、眼科と泌尿器科の病名のように共通病名が少ない2つの科の病名集合がこの条件に近い)。それぞれの病名の種類を \(N\) とする。2つの集合を合併すると、病名の種類は \(2N\) になる。2つの集合が同じ分布をして、全く同じ病名がないとすると、片方の集合の頻度が \(n\) 番目の病名は合併集合ではその頻度が \(2n\)(これを \(K\) とする)番目もしくは \(2n-1\) 番目になる。その頻度は \(1/n\) である。すなわち頻度順が \(K\) の病名の頻度 \(Y_K\) は、\(Y_{K} =Y_{2n} =1/n=2/2n=2/K=Y_{2n-1}=Y_{K-1} \) となる。よって \(n\) の大きいところでは漸近的に同じZipf指数を持つZipfの法則に従う。しかし、頻度の高いところ(言い換えると \(K\) の小さいところ)ではZipfの法則からずれる。図Ⅲ-4-2に5つの共通病名のない集合を合わせた場合のグラフを表示している。頻度が低いところでは確かに、直線に漸近するのがわかる。しかし、頻度の高いところでは予想直線からずれ、頻度がより小さくなるのがわかる。

上記の例はいくつかのZipfの法則に従う集合を合併すると漸近的にはZipfの法則に従うが、頻度の高いところではZipfの法則からずれることを示している。実際の病名集合においても、頻度の高いところではデータ点が予想直線より小さい値になる。 この事は、今回、解析の対象とした病名集合(総病名,科毎病名、医師毎病名)がZipfの法則に従う小さな病名集合の合併集合である可能性を示唆する。
データの2番目の特徴として、日本語表記病名のZips指数に比べ、コード病名群のZipf指数の値が大きいことである。その原因としてのコード化の影響について考えてみよう。病名をコードで表すことに比べ日本語で表す場合、表記のゆれが起こり同じ病気に対してもいろいろな病名がつけられる33。そのため病名の種類が多くなる。すなわち、コード化とは複数の病名を1つの病名にまとめる効果がある。逆に、1つのコード化された病名は普通の日本語で表記すると複数のより細分化された病名に分解される。この時、新しい病名で考えたときの病名集合の頻度分布がどのように変わるかを考える。まず、1つのコード病名が一定の数の病名に分かれて、分れた病名の頻度がみな等しいと仮定する。この場合新しい病名集合はやはりZipf集合を成すが \(\zeta\) は変化しない。このことは、重なりの無い2つのZipf集合を合併すると同じ \(\zeta\) を持つZipf集合が出来ることと同様に示すことが出来る。
次に、1つの病名を分解して出来た個々の病名集合がそれぞれZipf集合になると仮定した場合を考えてみよう。文章などの単語分布がZipfの法則に従う理由は良く分からないが、同じ意味を表す多数の表記からの自由選択という行為がこの分布を導いている可能性がある。この意味で、自由表記による病名の場合も同じような原理が働き、それがZipf分布をする可能性は十分考えられる。
コード表記による病名の集合を考える。頻度が \(x\) 番目の病名の頻度 \((Fx)\) が
\begin{eqnarray}
F_{x}=\left [\frac{A}{x}\right ] \quad x=1, 2, \ldots \tag{Ⅲ-4-1}
\end{eqnarray}
で表されるとする(ここで\([\quad]\)は小数点以下の切り捨てを表す)。ここで、おのおのの病名がいくつかの病名に分解され、その分解された病名集合が再びZipf指数 \(\zeta\) が1であるZipf分布をすると仮定する。すなわち、\(x\) 番目の病名の頻度が \(F_x\) であるので、これが \(n\) 個の病名に分解したとする。
\begin{eqnarray}
F_x=\sum_{j=1}^{n} \left( \frac{B}{j} \right) \tag{Ⅲ-4-2}
\end{eqnarray}
これを満たすような仮の \(B, n\) を次のように決める。
病名の最低頻度は1であるので、
\begin{eqnarray}
\frac{B}{n}=1
\end{eqnarray}
\(B=n\)を式Ⅲ-4-2に代入すると、
\begin{eqnarray}
F_{x}=\sum_{j=1}^{n} \left( \frac{n}{j} \right)=n\sum_{j=1}^{n}\frac{1}{j} \simeq n\int_{1}^{n}\left (\frac{1}{t} \right)dt=n\log{n} \tag{Ⅲ-4-3}
\end{eqnarray}
そこで \(n\) を次の条件を満たすように決める。
\begin{eqnarray}
n\log{n} \leqq F_{x} \lt (n+1)\log{n+1}
\end{eqnarray}
次に以下の式を満たす \(s\) を求める。
\begin{eqnarray}
F_{x}=\sum_{j=1}^{s}\left\{\left[ \frac{n}{j} \right]+1\right\} \tag{Ⅲ-4-4}
\end{eqnarray}
このようにして、x番目の病名をs個の病名に分解する。
このようにしたとき、頻度分布がどのようになるかをシミュレーションにより求めた。シミュレーションにおいては(Ⅲ-4-1)式において \(F_1=A=10000\) となるようなデータを使った。この時、もとの病名集合のZipf指数は0.97となる。この各病名を上記の方法で複数の病名に分解すると総病名種は19686種類、\(\zeta\)=0.67となった。
このように、各病名集合をZipf分布をする病名集合に分解するとすると、Zipf指数がより小さなZipf集合ができる。また、逆に病名のコード化とは上記と逆の過程であり、その頻度分布がZipfの法則に従う病名群をまとめて1つの病名として扱う過程であると考える事が出来る。もしコード化にこのような作用があるならば、コード化によってZipf指数が大きくなると考えられる。
このことをさらに実際のデータによって調べてみた。今回使用した病名コードは、より細かい分類に対応するため本来4桁であるICDコードに、2桁のコードを追加した6桁のコードになっている。そこで6桁のうち4桁コードだけで病名を区別したときどうなるかを調べた。その結果、同じようにZipf集合になるが、4桁の病名集合ではZipf指数はより大きくなった。これは、上記の仮定の正しさを証明している。
コード病名の解析において、内科の病名集合と総病名集合がZipfの法則からのずれが大きかった。このようなずれが起こった理由を考察しよう。まず、内科は他の科に比べて多様な病名を含んでいる。この事は、内科病名がより多数の基本的な病名の合併集合であることを示している。前述したように、共通部分の無いZipf集合を合併すると漸近的にはZipfの法則に従うが、頻度の高いところでは直線からずれる集合が得られる。内科では多数の合併が起こっている可能性があり、そのため頻度の高いところで大きく直線からずれてしまったと考えられる。総病名でも同じ事が起こると考えられる。もう1つの可能性は、病名の飽和である。コードによる病名では病名の種類が登録されたコードの種類に限定されている。今回使用した病名のマスターデータには12000程度の病名が登録されている。患者に付ける病名の種類が多くなり、このマスター上の病名数の上限に近づけば、病名の飽和が起こりZipfの法則からずれていく可能性がある。総病名の場合、病名の種類は3200を超えており、このような影響が出てきた可能性がある。
今回、病名集合を科、医師、ICD-10コードにより細分類を行ったが、それらのすべての集合においてZipf集合が得られた。このような異なる分類基準による分類すべてにおいてZipfの法則が成り立つことと、Zipf集合の和集合が再び漸近的にZipfの法則に従うという事実から、今回の解析における分類集合よりもより小さい集合レベルでZipfの法則が成り立っている可能性がある。もしそうであるならば、今回の解析における分類集合はすべてこの、要素的なZipf集合の和であらわされることになり、当然再びZipf集合となる。そのような要素集合の存在を証明するためには、病名集合が如何にして作られるかを示す構成論的方法によるモデルを構築し、解析することが必要である。
いままでの話は、多数の病気を診療する総合病院あるいは、総合内科の結果である。受診患者が限定される専門病院や大学病院のようなより専門性の強い病院での病名分布については異なる可能性がある。そこで、甲状腺専門病院における病名分布について調べた。その結果が図Ⅲ-4-3である。図の(A)は日本語で表記された病名の頻度分布、(B)は同じデータに付随するICDコードの頻度分布である。グラフ(A)のZipf指数は2.09、(B)のZipf指数は2.5である。総合病院での例と同じでICDコードでのZipf指数が大きくなっている。しかし、いずれのZipf指数も総合病院の値に比べて大きい。普通各患者は複数の病気を持つ場合が多い、総合病院のデータは患者が複数の病気を持つ場合には、それぞれの病気の数を数えた。専門病院へ来る患者は複数の病気を持っていてもその病院で扱う病名のみを登録している可能性がある。そのため、コード化と同じ現象が起こり、Zipf指数は大きくなったと考えられる。
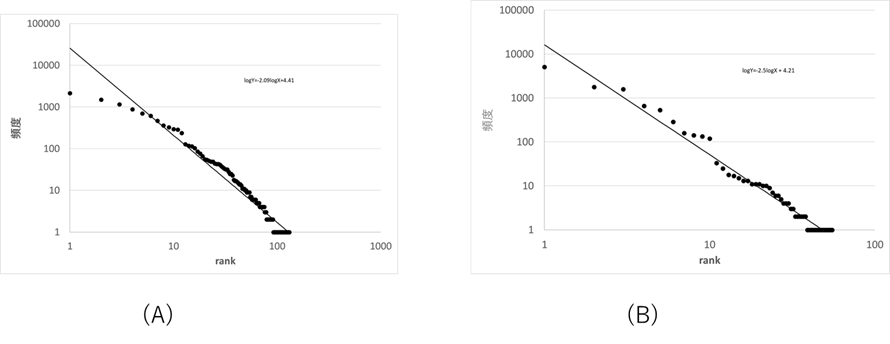
A:日本語病名
B:同じデータのICDコードによる頻度
2.病名づけは文脈(context)に依存する
病名というのは、その全てが並列的に存在するわけではない。病名によっては互いに強い結びつきのある場合もあり、また、あまり関係のない病名もある。例えば、ここに普通感冒の症状を持つ患者がいるとしよう、この患者の病名として、普通感冒、上気道感染、急性鼻炎、急性咽頭炎、急性気管支炎などが付く可能性がある。これらの病名は、容易に他の病名に移行する(もしくは、付け間違えられる)という意味において近い関係にあると考えられる。しかし、大腿骨骨折と上気道感染が移行するとは考えられないので、この2つの病名は遠い関係にあると考えられる。もちろん、2つの病名が互いに近いとか遠いとかいう関係は、その病名を見る尺度によって異なる。病因的に近い場合、症状的に近い場合、重症度において近い場合、社会的影響が近い場合など多くの尺度が考えられる。医師が患者を診る場合、どの尺度を使うかはそのときの状況(初診、特殊な検査時、入院中、患者の社会的立場、治療開始・途中など)によって異なると考えられる。しかし、その都度何らかの尺度を持った状態で患者を診ていると考えられる。そのときに持っている尺度によって、近い関係にある病名同士は診断に際して移行していく可能性がある。このような近い関係の病名を集めたとき、その病名集合がZipfの法則に従うと考えられるのではないだろうか。
例えば、ある1つの患者の状態に対して、つけられる病名が互いに近い関係の病名集合の1つであるとする。しかも、病名の持っている曖昧さによりどの病名を付けるかの絶対的基準がない場合がある。このような時、これらの内どの病名を付けるかは、医師の自由意思による選択に依存する。この状況は、文章をつくる時の単語の選択と同じ状況になると考えられる。そのため、これらの病名集合はZipfの法則に従うであろう。このような集合が病名の要素集合であると考えられる。
病名というのは、患者に対して医師が観測を行い、その結果病名が付けられる。その際、医師の知識、診断に際し医師が使う検査器具などの道具、患者のおかれた社会的状況などの環境に影響される。このように、病名というのは、客観的事実がはじめからあるのではなく、患者、医師、環境との間の相互作用の産物と考えられる。したがって、患者が同じでも医師や環境の状態を変化させるだけで出力である病名が変化する可能性はある。このことは観測の方法を変えると病名分布が変わることを示唆している
病名は、いろいろな観測状況に依存して生まれてくる。観測状況として、極端に異なる2つの状況がある。1つは、一般の診察である。医師は、患者の訴え、状態からほぼ無限といえるほどの病名から1つの病名を選ぶ。もつ1つの状況は、癌検診などにおける病名のつけ方である。この場合は、患者を診た医師はいくつかの少数の病名から1つの病名もしくは、異常なしという病名を選ぶ。この2つの観測を同じ患者集団に対して行った場合に、病名頻度はまったく異なったものになるであろう。
Zipfの法則に従う集合では、ある項目の頻度が集合の大きさによって変わる。また、集合全体の頻度の平均や分散も集合の大きさで変化する。このような状況は従来の考えではなかなか受け入れられない。しかし、上記の考察から、病名頻度は集団に対する観測状況によって変わる可能性が考えられる。これは、サンプル集団から外延した病名頻度という測度が本来存在しないことを意味するかもしれない。これは、フラクタルの発見によって曲線の長さや面積の存在しない図形という概念が出現した状況に似ている。
3.複雑ネットワーク
3-1 ネットワークの定義
前節において、病名は患者、医師、環境の間の相互作用によって決まると述べた。病名決定のための環境として最も重要なものは医師の病気に対する知識である。知識構造が病名決定において重要であるのは当然であると考えられる。知識構造の病名決定への影響を調べるには、まず病気あるいは医療における知識構造を調べる必要がある。知識構造を調べるにはいろいろな方法があると思われるが、その一つとして、知識のネットワーク構造という考えがある。知識のネットワーク構造の詳しいところは次節に解説するが、まず前提としてネットワークの知識が必要である。「ネットワーク」というのは数学的にはグラフと呼ばれている。ネットワークは主に物理や社会科学で使われる言葉であり、グラフというのは主に数学において使われるが、どちらも同じ意味である。
複雑系のような集団を扱う場合には、集団の要素の間の何らかの関係が問題となる場合が多い。細胞内の化学反応を調べる場合には、どの化学物質(要素)がどの化学物質と化学反応をするのかという関係が問題となる。人間集団を扱う社会学においては人間という要素が互いにどのような関係にあるかが問題となる。その関係としては友達関係、仕事内の繋がりなど非常に多様な関係が考えられる。このような要素とその要素の関係を抽象化したものがネットワーク(グラフ)である[66][67][68][69]。
ネットワーク理論では要素のことを頂点(nodeあるいはvertexとも呼ぶ)と呼び、各頂点の間の関係を枝(linkあるいはedgeとも呼ぶ)と呼んでいる。それで形式的にはネットワークとは次のように定義されている。
定義:ネットワークとは二つの集合 \(V\) と \(E\) の組 \(G\equiv (V, E)\)のことである。ここで、\(V=\{v_1, v_2, \cdots, v_N\}\) は頂点の集合で、\(E=\{e_1, e_2, \cdots, e_N\}\) は枝の集合である。枝とは二つの頂点のペア \((v_i, v_j)\) のことである。
これが、数学的な定義であるが、要は図Ⅲ-4-4のようなものである。この図で数字が付いた〇が頂点で、頂点間を繋いだ線が枝である。丸に付けた数字が頂点番号である。
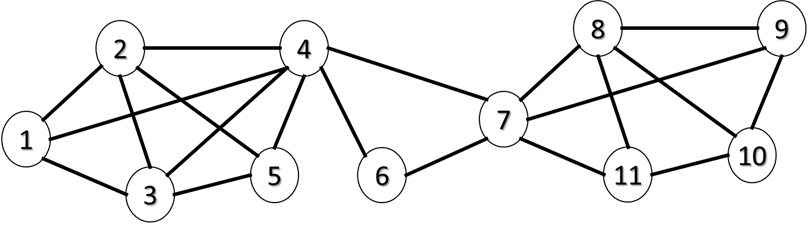
ネットワーク理論ではこのようなネットワークの色々な性質を調べている。例えば、二つの頂点の間の最短距離(二つの頂点を繋ぐための最小の枝の数)を求めたり、ネットワーク全体の直径などを求めたりする。
3-2 ネットワーク理論の指標
ネットワーク理論で使われる重要な指標があるので、以下に説明する。
二つの頂点 \(i, j\)の間が枝によってつながっているとき、枝の列を経路と呼ぶ。
例えば、図Ⅲ-4-4では頂点 1と4の場合、枝の列、\((1, 2), (2, 4)\) は頂点 1と4の間の経路である。ほかにも、\((1, 3), (3, 5), (5, 4)\) も経路である。一般には二つの頂点間の経路は多数存在する。
ネットワークが連結であるというのは、任意の二つの頂点間に経路が存在するときである。
要するに、全ての頂点が枝で繋がっているということである。図Ⅲ-4-4は連結なネットワークである。この図で頂点4と6,7の間の枝が無ければ、連結ではなくなる。
頂点 \(i, j\) の経路長の最小値を二つの頂点 \(i, j\) の距離と呼び \(l_{ij}\) と表示する。
ネットワーク内の任意の二つの頂点間の距離の最大値。ネットワークが連結ではない時には直径は無限であるとする。
ネットワークの平均最短長とはすべての頂点の組の距離の平均と定義する。
すなわち、頂点の総数を \(N\) とすると、
\begin{eqnarray}
\langle{l}\rangle \equiv \frac{1}{n(n-1)}\sum_{i, j}l_{ij} \tag{Ⅲ-4-5}
\end{eqnarray}
頂点 iの次数 \(k_i\) とは \(i\) から出ている枝の数のことで、\(k_i\) と表示する。
また、頂点 \(i\) につながった頂点を \(i\) の近傍(neighbors)と呼ぶ。
ネットワークにおいて次数 \(k\) を持つ頂点の確率と定義する。すなわち、
\begin{eqnarray}
p(k) \equiv \frac{次数 k をもつ頂点の数}{N} \tag{Ⅲ-4-6}
\end{eqnarray}
ネットワークの全てのnodesの次数の平均。
\begin{eqnarray}
\langle k \rangle \equiv \frac{1}{N}\sum_{i=1}^{N}k_i =\sum_{k=0}^{\infty}kp(k) \tag{Ⅲ-4-7}
\end{eqnarray}
頂点 \(i\) のクラスター係数 \(C(i)\) は次のように定義される。
\begin{eqnarray}
C(i) \equiv
\begin{cases}
\displaystyle\frac{e_i}{k_i(k_i-1)/2} & (k_i \gt 1) \\ 0 & (k_i \leq 1) \tag{Ⅲ-4-8}
\end{cases}
\end{eqnarray}
ここで、\(e_i\) は \(i\) の近傍間にある枝の数
これは、頂点 \(i\) の近傍の頂点間の可能な最大枝数に対する、実際の近傍間の枝の割合を表す。もしくは、頂点 \(i\) とその近傍との間にできた三角形(辺は枝)の、全ての近傍同士が枝で結ばれていたとして時にできる三角形の数の割合である。直感的には、近傍同士がどの程度繋がっているかという指標。社会的にはある人の友達同士が互いに友達である確率。
各頂点のクラスター係数の平均である。
\begin{eqnarray}
\langle C \rangle \equiv \frac{1}{N}\sum_{i=1}^{N}C(i) \tag{Ⅲ-4-9}
\end{eqnarray}
直感的にはある集団内の個人が互いにどの程度密接に関係しているかという指標。平均クラスター係数が大きいとは、新しく人に出会ったとき、その人と自分との間に共通の知り合いがいる確率が大きいということである。
3-3 ネットワークの例
1.完全グラフ(complete graph)
すべての頂点同士が枝で結ばれているネットワーク
2.格子(lattice)
頂点と枝で格子を成しているもの。
3.ランダムグラフ(Erdős-Rényi graph)[67][70][71][72][73][74][99]
頂点が \(N\) であるネットワークで、各頂点間に枝がある確率が \(p\) であるようなネットワークで、
\(G_{n, p}\) と表される。
表Ⅲ-4-2はそれぞれのネットワークの性質の要約である。ここで、特にRandom graphの \(\langle l \rangle\) (平均最短長)と \(\langle C \rangle\) (平均クラスター係数)が重要である。
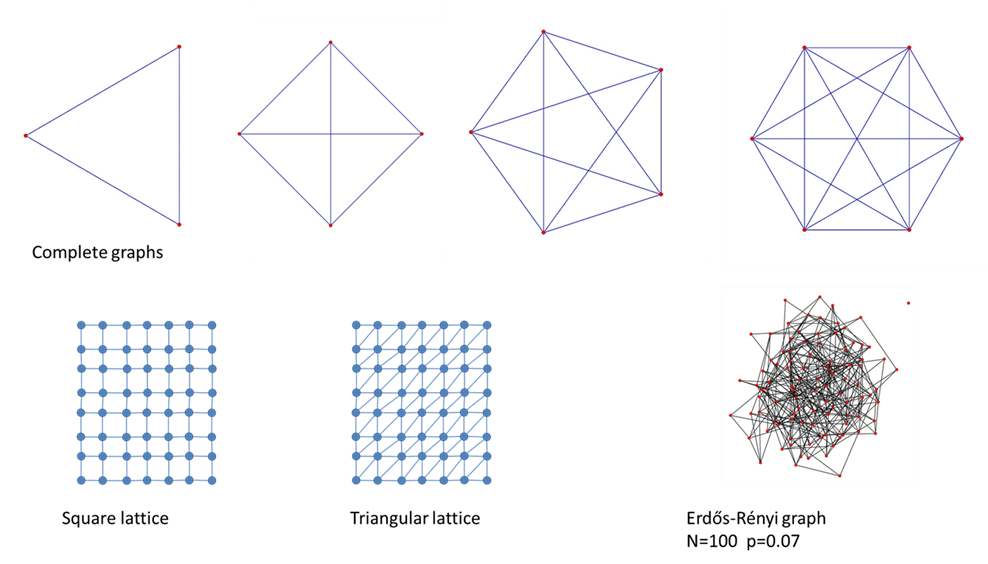
ネットワーク理論が複雑系の中で注目されたのは、ネットワークのsmall world性とscale free networkの概念が出てからである。
Small World Network
ネットワークがsmall worldであるとは[78]、1)ネットワークの頂点数 \(N\) が大きくなるにつれ平均最短長が\(\log{N}\) 程度にしか増加しない、2) \(N\) が増加しても平均クラスター係数がゼロにならない、の二つの性質を持つことである。この二つの性質はRandom graphとの比較で定義されている。表Ⅲ-4-2を見ればわかるように、Random graphは平均クラスター係数は \(N\) が大きくなるとゼロになる。また、頂点間の平均最短長は \(N\) の増加とともに \(\log{N}\) 程度に増加していく。Small world networkというのは平均最短長がRandom graph程度であるが、平均クラスター係数はRandom graphより大きいネットワークという意味である。
Small world[79][80][81]というのは、元々はMilgram等が行った実験に基づいている。アメリカに住む無作為に選ばれた人を始点として、ボストンに住む目標人物まで手紙をリレーして届けるという実験である。各人はファーストネームで呼び合うくらい親しい人に手紙を送る。送られた人は、同じように親しい人に手紙を送る。そうして、最終的に目的人物に手紙が届くかを実験した。すると、平均6人を介して手紙が届いた。これを評して6次の隔たりと呼んだ。このことから、アメリカの任意の二人は6次の隔たり以内でつながっているという結論を導いた。たった、6人を介すればだれにでもつながるという意味でこの現象をSmall worldと呼んだ。2億人以上の人口のアメリカにおいてたった6人を介すればつながるという事実は人々を驚かせる結果であった。
ところで、一億の対数は \(\log{100000000}=8\) である。上記の6次よりは少し大きいが、大体ネットワークがsmall worldの性質を満たせば、6次の隔たりという現象を説明できる。
| Complete Network | Lattice | Random network \((N, p)\) | ||
| square lattice | triangular lattice | |||
| \(k_i\) or \(\langle k \rangle\) | \(N-1\) | 4 | 6 | \(Np\) |
| \(\langle l \rangle\) | 1 | \( \approx \sqrt{N}\) * | \(\approx \frac{\log{N}}{\log{\langle k \rangle}}\) | |
| \(\langle C \rangle\) | 1 | 0 | 2/5 | \(\approx \frac{\langle k \rangle}{N}\) |
| \(P(k)\)* | \(\delta_{k, N-1}\) | \(\delta_{k, 4}\) | \(\delta_{k, 6}\) | \(\approx \frac{e^{-\langle k \rangle}\langle \lambda \rangle ^k}{\langle k \rangle !} (\lambda = Np)\)** |
* 二つの関数 \(f(n)\) と \(g(n)\) があって、\(\displaystyle\lim_{n \to \infty} \frac{f(n)}{g(n)} =A \) となり、\(A\) が正の数であるときに
\(f(n) \approx g(n)\) と書く。
** Random graph \((N, p)\)
\(\displaystyle P(k)=\frac{(N-1)!}{k!(N-1-k)!}p^{k}(1-p)^{N-1-k}\)
ここで、\(N\) が大きく、\(p\) が小さくて \(\lambda = Np\) が適度な大きさであるときには、\(P(k)\) はポアソン分布になる。すなわち、\(\displaystyle P(k)\approx \frac{e^{-k}\langle \lambda \rangle^{k}}{k!}\) となる。
Scale free network
Scale-freeネットワークとは、ネットワークの次数分布がベキ分布に従うようなネットワークのことである[82][83][84]。すなわち、
\begin{eqnarray}
p(k)=Ak^{-\alpha} \quad (k \gt k_{min}) \tag{Ⅲ-4-10}
\end{eqnarray}
となる。第2章で説明したように、ある値 \(k_{min}\) 以上のところでベキ法則にしたがう分布であり、\(\alpha\) のことをベキ指数と呼んでいる。次数分布がベキ法則に従うネットワークは多くある。代表的なものとしてはWWW(World Wide Web)[85]、言語ネットワーク(文章中の単語を結んでネットワークとしたもの。第4章-4参照)、actor networks などがある。スケールフリーネットワークを作るモデルはいくつか提案されているが、最も重要なものはBarabási とAlbertによる preferential attachment modelと呼ばれるものである[82][83][84]。これは、2章で述べたYule process(rich-get-rich)のネットワーク版である。具体的には次のようなモデルである。
1)\(m_0\) 個の頂点からなる完全グラフを作る。
2)各時点で \(m\) 本(\(\leqq m_0)\) の枝を持つ頂点を1つ追加する。これらの、枝はすでに異なる \(m\) 個の頂点につなげる。このとき、頂点 \(i\) につなげる確率は頂点の次数 \(k_i\) に比例するとする。すなわちその確率を \(\pi_i\)とすると、
\begin{eqnarray}
\pi_{i}=\displaystyle\frac{k_i}{\sum_{j=1}^{N}k_i} \quad (1 \leq i \leq N) \tag{Ⅲ-4-11}
\end{eqnarray}
となる。
このモデルで \(t\) ステップ後には、\(t+m_0\) 個の頂点と \(mt\) 本の枝を持つネットワークができる。このモデルをシミュレーションするとスケールフリーネットワークができる。その際のベキ指数は \(\alpha=2.9\) となった。理論上は \(\alpha=3.0\) となる。実際の世界にあるスケールフリーネットワークのベキ指数が2~3であることから、このモデルのベキ指数は少し大きめである。しかし、モデルを少し変えることによってこの指数は変化させることができるので、ベキ指数の大きさについては大きな問題ではない[86][88][89][90]。重要なことは、スケールフリーネットワークの生成において、ネットワークの成長過程でpreferential attachment(優先的選択)が起こることである。
Preferential attachment modelでは、次数分布は完全なベキ分布となる。しかし、実際のスケールフリーネットワークは大きな次数の場所でベキ分布から外れることが多い。このような、ベキ分布から外れる分布は2章で述べた「切り捨てベキ分布」(truncated power law)である。Preferential attachment modelに何らかの制限をつけることによりこのような切り捨てベキ分布が得られる[18][91][92][93]。
スケールフリーネットワークの平均最短長はsmall worldの条件である \(log{N}\) 程度にしか増加しないという条件はもともと満たしている。しかし、クラスター係数については一般に満たしてはいない。クラスター係数もsmall worldの条件を満たすようになるネットワークモデルは多数提案されている[58]。その中で重要なものは階層性のあるモデルである[89]。階層性モデルとは階層的な規則もしくは再帰的な規則によって作られたモデルという意味である。再帰的というのはここでは深くは述べないが、フラクタル図形を作る時に使われる構成法でもある[4]。
図Ⅲ-4-6にRavaszによる階層モデルの作成法の図を載せておく。Step0の図を三つ赤い頂点につなげる(step1)。次にこのstep1の図を3つこの先端につなげる(step2)。これを繰り返していく。このネットワークは決定論的モデルであるが、新しい図を繋げるときに優先選択の要素を入れれば、前述のpreferential attachment modelが出来上がる。階層モデルにはスケールフリーであること以外に以下の二つの特徴がある。
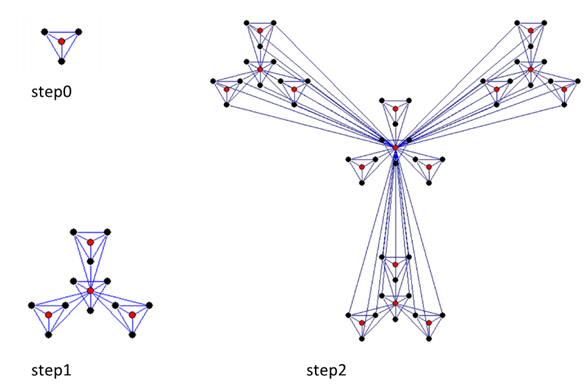
Ravaszの論文[89]内の図を筆者が改変
現実の世界にあるWWWなどの大規模ネットワークは全てスケールフリーでスモールワールドの性質を持っている。さらに、階層構造を持つものも多い。これらをまとめて扱うために複雑ネットワークの概念が生まれた。複雑ネットワークの正確な概念は未だあいまいであるが、一般にはスケールフリーでスモールワールドの性質を持つネットワークを意味する場合が多い[66][94][95]。ただ、あくまでも現実の世界に見られる大規模ネットワークの研究のための用語であるので、定義自体は今後も変化する可能性がある。
複雑ネットワークという言葉における複雑という言葉であるが、これを明確に定義した文章を見つけることはできなかった。ただ、一般に複雑ネットワークの対象の系は大規模で複雑系である場合がふつうである。その意味で複雑ネットワークの複雑は複雑系の意味であると解釈してもよいであろう。
生物や医療関係でも多くのスケールフリーネットワークが見つかっている。医療知識ネットワークについては次節において説明するので、ここでは生物、医療関係でみられるスケールフリーネットワークのいくつかの例を説明する。
細胞内では多数の化学成分同士が化学反応(代謝)を行っている。これらの化学成分同士がどのような化学反応を行っているかのネットワーク(代謝ネットワーク)をJeongなどが調べている[88][90]。その結果、代謝ネットワークはスケールフリーでスモールワールドの性質を持つことが分かった。多くの種について同じことを調べたところ、それらの種でも同じような構造を示しており、これらの性質が一般的であることが示された。さらに、スモールワールド性に関しては、半径がネットワークの大きさNに対して、\(\log N\) で変化するのではなく、\(N\) が大きくなっても半径はほとんど変化せず、3前後である。これは、スモールワールド性よりも強い特徴である。生物は半径を大きくしないように進化の過程で保っている可能性があると述べている[88]。このことは次の節で説明する医療知識のネットワークにおいても成り立っている。また、Ravatzは同じように、種ごとの代謝ネットワークを調べた[90]。その結果、全ての種で、代謝ネットワークは小さな緊密に結びついたネットワークからなる多数のmoduleから成り立つことが示された。これらの、modulesは階層構造によって、より大きいが緊密性に欠けるunitsを構成する。またUnitsの数やクラスター係数にはベキ法則が成り立つ。このとき階層性の証明としては上記に示した階層構造を持つネットワークの特徴である、\(C(k)\approx \frac{1}{k}\) という結果を使っている。
もう一つ医療分野で重要なスケールフリーネットワークは感染症である。もともとは、Lilijerosらがスウェーデンのランダムに選ばれた4781人の性行動を調べたのが始まりである[96]。これは、HIVなどの性感染症がどのように広がるかという疑問に答えるためである。その結果、調査日から12カ月以内に一人の人が性関係を結んだ人数の分布はベキ法則を満たし、そのベキ指数は約2.4であった。すなわち、性行動ネットワークはスケールフリーを成すことが証明された。この調査はHIVなどの性感染症の伝播についての新しい知見を与えた。性行動に伴って広がる性感染症は全ての人が平等に他の人に移すのではなく、ある特定の人が非常に多くの人に感染させるという特徴を持っている。スケールフリーネットワークによる感染症の伝播は平等に他の人に移すRandom networkとは異なるスピードで広がる。また、伝播の広がりを抑える方法も、スケールフリーネットワークの場合は普通とは異なる方法が必要である。伝播を抑えるにはすべての人に等しく感染抑制の教育などするのではなく、多くの人に感染させる人に対する重点的教育の方が効果が大きい。
上記の感染症対策は、スケールフリーネットワークの特性から説明することができる。Albert等はスケールフリーネットワークの脆弱性について調べている[97]。連結なネットワークはその中の頂点や枝を除いていくとどこかで連結性が失われ、壊れてしまう。除く数が少なくて連結性が失われるときにはネットワークは脆弱であると表現する。Albert等によれば、「スケールフリーネットワークはランダムに選ばれた頂点に対する攻撃(perturbation)には強い(ネットワークが壊れにくい)が、攻撃が枝をたくさん持つ頂点に対して選択的に起こるならばネットワークは虚弱である。」と述べている。これは、まさに上記の性感染症の予防のための戦略に一致する。
2019年から起こった新型コロナウィルス感染症において、スーパー・スプレッダーという言葉が有名になった。これは、SARSや今回のコロナウィルスにおいては各人が平等に他の人に病気を移すのではなく、一部の人は非常に多数の人を感染させ、他の人はあまり感染させないという事実から生まれた言葉である。前記の性感染症の場合と同様、新型コロナやSARSにおいても、多数の人に病気を移す人という意味でスーパー・スプレッダーという言葉が使われている。このことは、性感染症以外の感染症もその伝播ネットワークがスケールフリーを成している可能性を示唆している。このようなスケールフリーネットワークの感染症はスーパー・スプレッダーに対して個別に予防処置をした方が効果的である。その方法が「クラスターつぶし」と呼ばれているものである。
スケールフリーネットワークの感染症への応用については増田他「複雑ネットワーク」[11]に詳しい。
4.医療知識ネットワークと病名分布 [98][99]
前に述べたように(第4章-2)、病名というのは、客観的病名がはじめからあるのではなく、患者、医師、環境との間の相互作用の産物と考えられる。この環境の中でも医療知識というものが重要であると思われる。そこで、医療知識の構造を調べる必要がある。しかし、そもそも医療知識とは何を意味しているのであろうか。数学などの場合、まず、言葉の正確な定義があり、その定義に基づく明確な論理が存在する。物理学も基本的には同じ構造を示している。最初に質量の定義があり、それが支配する運動方程式という形で整理されている。それに対して医学あるいは医療においては、非常にあいまいである。使われる言葉も割と自由であり、しばしば新しい言葉が作られていく。また必要無くなればその言葉もなくなっていく。多くの言葉の定義もあいまいで、全体の文章の中で何となく定義される場合も多い。一度定義された病名でも時代とともに変わっていく。
一例として症状の一つである「痛み」について考えてみる。痛みと発熱で新規の外来患者の大半を占めると言われるほど痛みは普通にみられる症状である。この痛みという概念は、医学における概念の曖昧さ、あるいは多様性をよく示している。痛みとは古典的には知覚の一種である。痛みは、触覚、冷覚、温覚と並んで知覚の一部である。傷などの障害があると対応する受容器が刺激され、その刺激が神経を伝わって中枢へいく。中枢において痛いと感じる。これが、古典的な痛みの概念である。この痛みの概念はデカルトによって既に述べられている。デカルトはこのような肉体の痛みとともに、心の痛みという概念も述べている。特別な傷害が無くても、うつ病などの心の病を持つ人は痛みを訴える。このような痛みを心の痛みと分類した。
痛みが単純に肉体の痛みと心の痛みに分類されるならば、少なくとも肉体の痛みに対する対処法は単純である。痛みを取るには原因の傷害を無くす、痛みの受容器を麻痺させる、伝達する神経を遮断する等の対処法がすぐに思いつく。このような対処で、痛みの原因はともかく痛みという症状自体をコントロールすることは容易なはずである。アスピリンなどの鎮痛解熱剤は、痛み受容体の疼痛閾値を上昇させることにより鎮痛効果を表す。キシロカインなどの局所麻酔薬は神経伝達をブロックすることで痛み刺激の伝達を抑制する。モルヒネなどオピオイドと呼ばれる物質は脊髄における痛覚伝達の抑制や視床や大脳皮質知覚領域などの脳内痛覚情報伝導経路の興奮抑制などによって鎮痛効果を示す34。
これら多数の鎮痛薬が開発され、痛みそのもののコントロールは容易であると考えられた。しかし、多数の鎮痛薬が開発されても、痛みで苦しむ患者数(普通には肉体の痛み)は一向に減少しない。さらに、上記の古典的な痛みのメカニズムからは考えにくい痛みも多数発見されている。
コルドトミーと呼ばれる鎮痛のための処置がある。これは痛み伝導路である脊髄の外側脊髄視床路と呼ばれる経路を外科的に切断する手術である。この切断によって痛み信号の伝達が遮断されるため、切断部以下の鎮痛が得られるはずであった。しかし、この手術を受けた患者の一部に、痛みの再発や痛みの増加がみられる例が多く出ている。
皮膚に水疱ができ痛みが起こる病気に帯状疱疹という病気がある。帯状疱疹自体は免疫不全でもない限りほぼ自然治癒する病気である。しかし、帯状疱疹が治癒した後、1カ月以上して同じ部位に痛みが起こることがある。これが、帯状疱疹後神経痛と呼ばれる病気である。帯状疱疹自体は治っているが、その病気の際に神経が傷ついて痛みが持続すると考えられている。何らかの外傷が起こり、外傷が治癒後1カ月以上して起こる痛みがある。昔はカウザルギー、現在は複合性局所疼痛症候群(complex regional pain syndrome: CRPS )と呼ばれている病気である。この病気も痛みの原因と考えられる外傷が完全に治癒した後の痛みである。もっと不思議な痛みとしては四肢の切断後に起こる幻肢痛がある。これも当然ながら痛みを起こす原因が見つからない痛みである。これらの痛みはいずれも痛みを起こす原因がはっきりしない病気である。そして、いずれも普通の鎮痛剤や神経ブロックなどは効果が小さい。場合によっては交感神経のブロックや抗うつ薬などの方が大きな効果を示すことが多い。
このように、肉体の痛みと考えられる痛みに関しても、従来の考え方では対処できない痛みが存在している。さらに、明らかに痛みを起こす原因があると思われる状況でも痛みを感じない例もみられる。有名なものとしては戦場における痛みである。戦場においては重傷を負っているのに、痛みをあまり訴えない兵士が存在する。また、犬に対して、痛み刺激を与えると同時に餌を与えるような操作を繰り返し行うと、痛み刺激に対して痛み行動を起こさなくなる、といわれている。戦場の例では、負傷することは戦場から家に帰れるということを意味し、そのことが痛みを抑制するといわれている。また、犬の実験では餌をもらえるという喜びがやはり痛みを抑制するといわれている。
そもそも、人間は「痛み」という感覚あるいは言葉をどのようにして学習したのであろうか。ある人が「痛い」と訴えた時の痛みは、他の人の「痛い」という感覚と同じなのであろうか。このことに関して丸太に従い述べてみよう[100]。人間がそもそも痛いという感覚を感じる、あるいは痛いという言葉を覚えることをどのようにして獲得するか、ということが問題である。赤ん坊がある時、転倒してしりもちをつく。この時、いわゆる痛みの感覚を経験するのであるが、この感覚を痛みと解釈するためには学習が必要である。転倒した時に、母親が抱っこして「痛かったね、痛いの、痛いの、飛んでいけ」と声をかけるかもしれない。このような声掛けを何度も繰り返すと、この転倒した時の感覚が「痛い」という感覚であると子供は学習する。このような学習を転倒以外の痛み感覚に対しても繰り返し受けることによって「痛み」という感覚を身に着けると考えられる。
痛みは純粋に主観的な感覚体験である。そのため、他人の痛みは分からないはずである。しかし、多くの人は、ある人が痛いと叫んだ時に、同じように痛みを感じることができる。これは、多くの人が同じような経験を繰り返すからである。みんなが転倒した時に母親から「痛い」という言葉を教えられることによって、痛みという感覚が人々の間に共有され、「痛い」という感覚が共通の言葉として理解されるようになる。
しかし、母親の対応は皆が同じというわけではない。例えば、次のような状況を考える。幼児が他の子供に突き飛ばされ、転倒して膝を擦り剥くとする。このような時、幼児は痛みとともに、驚き、悲しみ、不安、悔しさなどの感情を抱くだろう。これに対して、母親によって対応が異なるとしよう。母親Aは怪我に驚いて、怪我の治療だけを一生懸命して、「もう痛くないわよ」という。母親Bは「突き飛ばされて、悔しくて、悲しかったのね」と言って抱きしめる。母親Aのような対応をいつも受けていた幼児は、驚き、不安、悲しみ、悔しさなどの感情をすべて痛みであると認識するかもしれない。
次のような例も考えられる。ある幼児が悪いことをして、叩かれるとする。このようなことが繰り返されると、悪いことをしたという罪悪感が痛みに転化するかもしれない。
つまり、「痛み」という感覚は生得的にあるわけではなく、学習によって得られるということである。打ったり、転んだりといった、皆に共通の経験を学習することで、その時の感覚として「痛い」というラベルがつけられる。しかし、学習は人によってそれぞれちょっとずつ異なっている。そのため、人によっては「痛み」のなかに、不安、悲しみ、罪悪感、驚き等の感情が混在する。そのような人が痛みを訴えた場合、それは罪悪感の表れなのかもしれない。このような人に鎮痛剤を使っても、痛みは改善しないだろう。
このような経過を得て、現在、ペインクリニックの世界では、痛みは次のように定義されている。
「痛みは症状である。痛みは「いたい」という主観的な知覚体験である。」
この定義は、ある意味何も述べていない。まるで、定義することを放棄したような定義である。しかし、こうでも言わないと定義できないということを表している。
長々と痛みという概念について語ってきたが、これは、医学や医療の世界における、概念のあいまいさを説明するためである。数学や物理などと異なり医学や医療の世界では概念は厳密に定義して使われることは少ない。痛みという概念についても、初期の古典的な痛みの概念と心の問題まで含める現代的な痛みの概念はずいぶん異なっている。数学や物理などではこのように概念が大きく変更するならば、ふつうは新しいことばが作られる。昔の痛みと現代の痛みという形で痛みの概念を新たに作るという考えもあり得る。しかし、医学や医療においては、普通そのようなことは行われない。なぜなら、医学や医療においては概念は日々変動しているからである。また、医学者だけで概念を変更することは出来ない。「痛み」という症状を訴えるのは患者である。「痛い」と訴えて来院した患者に、それは痛みではありませんと言っても仕方がないことである。医学や医療の世界は、患者という現実の世界と常に接点を持っている学問である。学問の都合でかってに言葉を変えてしまうことはできないのである。
では、このようにどんどん変更されていく概念の世界をどのように認識すべきなのであろうか。医学や医療で使う各種の概念は数学的な意味での定義をすることはできない。あくまでも一つの概念(ことば)はその概念に関係する言葉によって規定されている。古典的な「痛み」という概念は、傷害、受容器、刺激、神経、伝達などの言葉で規定されている。しかし、現代的な「痛み」という概念は、上記の言葉以外に、心、不安、情動、交感神経、罪悪感、抗うつ薬、社会なども「痛み」という概念を規定するために使われる。
ある概念やことばが、「ことば」によって規定されるという考えは、医学特有な考えではない。人間のことば、自然言語という体系自体が、そのような性質を帯びている[101][102]。医療知識とはこのように自然言語によって記述された体系であると考えられる。
では、体系的には組み立てられていないと思われる知識体系を調べるにはどうすればよいであろうか。近年、このような自然言語による記述に対して、その構造を分析するための方法が開発されてきた。その体系で使用されている単語同士を何らかの基準により結びつけネットワークを構成する。そのネットワーク構造をネットワーク理論の方法で分析するのである。この分析によって前述のスモールワールド性やスケールフリー性が言語の中にも出現することが分かっている[103][104][105] [106][107][108][109]。このような方法を使って、医学の体系を分析することが可能である。医学体系を記述したもの、例えば医学教科書の記述に対して自然言語分析の方法を使うのである。
筆者らは医学知識の記述の代表として内科学の標準的教科書であるハリソンの「内科学」(日本語翻訳版)を利用した[110]。まず、手作業により文章内の単語の整理を行い、医学的に意味のある一つの単語あるいは複数の単語からなるひとまとまりをtermとした[98]。単語そのものを扱わないのは、言語の構造を知るのではなく、あくまでも医学知識の構造を知るためである。各termは一つ或いは数個の単語から成り立っている。また、各termを診断名(\(d\))、自覚症状(\(s\))、他覚的異常(\(f\))、その他の医学専門用語(\(x\))に分類した。例えば、stomach cancerは二つの単語から成る病名に分類されるtermである。文章にはtermに含まれない冠詞、接続詞、動詞、副詞、形容詞なども含んでいるが、これらの単語は分析の対象から外した。このような方法により文から抜き出した各termをネットワークの頂点(node)とする。一つの文に含まれる各termを互いに枝によって結ぶ。このように、文章内のterm同士を枝で繋ぐことにより一つのネットワークを構成することが可能である(図Ⅲ-4-7)。このネットワークを以下、MKN(the medical knowledge network)と呼ぶことにする。
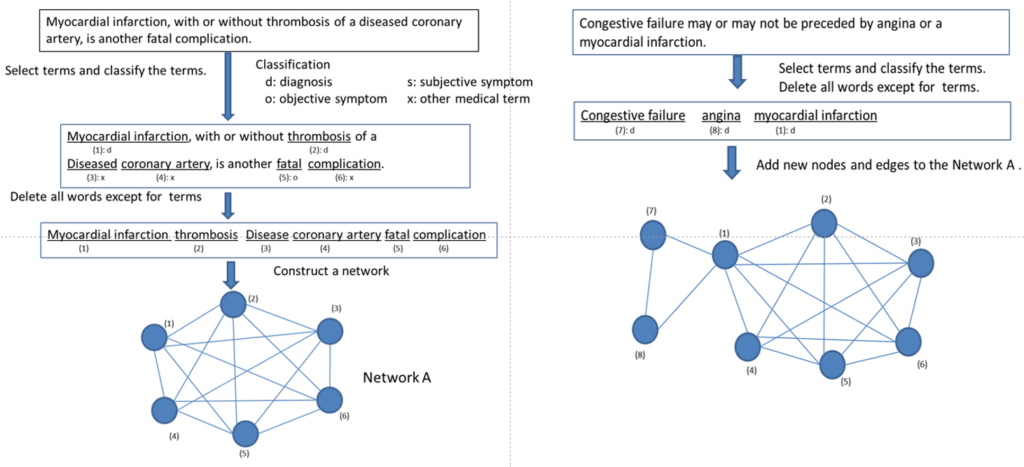
文献[98][99]
表Ⅲ-4-3はネットワーク分析の要約である。MKNネットワークにおける次数の平均は37、平均距離は4.317、クラスター係数は0.86である。短い平均距離と大きなクラスター係数というスモールワールドの特徴を示している。実際、MKNと同じ頂点数と枝の数をもつ対応するランダムグラフの平均距離は3.07でありクラスター係数は約0.0008である。このことから、構成されたMKNはほぼ対応するランダムグラフ程度の平均距離を持ち、ランダムグラフよりはるかに大きいクラスター係数を持つことがわかる。すなわち、MKNはスモールワールドであることが示された。

文献[98][99]
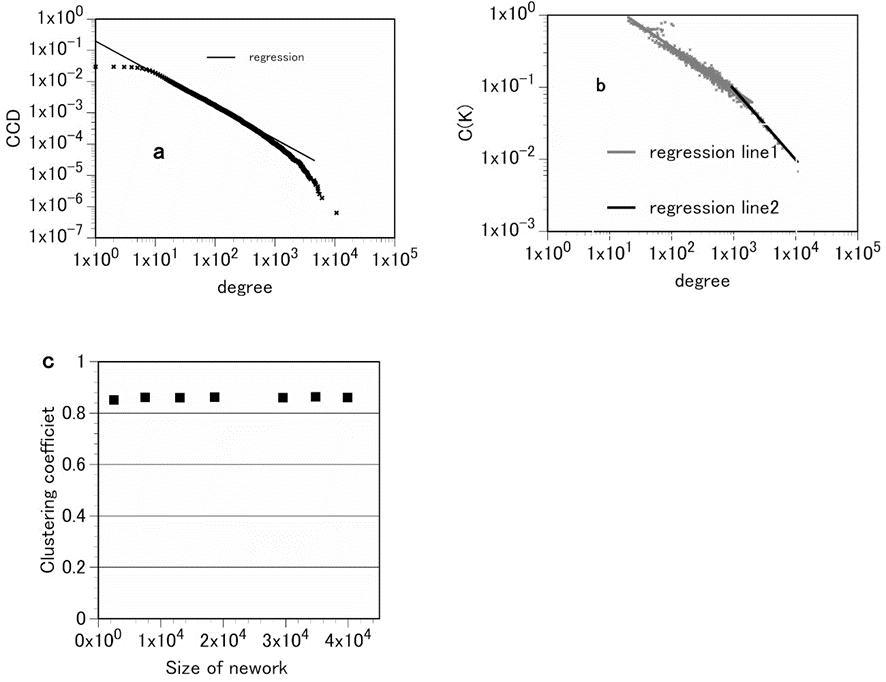
a.MKNの次数の相補累積分布(CCD)
b.次数kのnodesの平均クラスター係数(C(k))
c.ネットワークサイズによる平均クラスター係数の変化
文献[98][99]
図Ⅲ-4-8はMKNについての次数の相補累積分布(CCD)とクラスター係数の分布\(C(k)\)、異なるネットワークサイズにおける平均クラスター係数のグラフである。図からわかるように、MKNの次数分布はスケールフリーの特徴であるベキ分布(正確には切り捨てベキ分布)を示す。そのベキ指数は2.045である35。完全なベキ分布に比べて次数が大きいところでは直線からずれてくるが、これは4章-2で述べたネットワークの有限性の制限のためと考えられる。さらに、ネットワークの階層性についても調べた。前節で述べたようにRavasz等によると、ネットワークが階層構造を持つ場合のネットワークの性質として①クラスター係数がネットワークの大きさによらない(independent)こと、②次数が \(k\) のnodeの平均クラスター係数 \(C(k)\) が指数1のベキ法則(power-law)を満たすという二つの条件を挙げている[89][90]。そのことを示したのが、図Ⅲ-4-8のb.とc.である。図に示すように、MKNはRavaszの二つの条件を満たしているので、階層性を持つと考えられる。
以上の事実から、MKNはスモールワールドでスケールフリー性と階層構造をもつネットワークであることが示された。スモールワールド性は知識や情報の検索効率の点で有利である。医師が診療を行うときには膨大な知識から適切な病名を選び出す。医師は患者が示す症状や検査成績から数万個に及ぶ病名の中から素早く適切な病名を選ばねばならない。医療知識がスモールワールドの構造を持っていることは症状や検査成績からわずか5ステップ以内に適切な病名にたどり着くことができることを示している。医療知識がスモールワールド性を持つことはこのような連想を行う際に非常に有効であると考えられる。
一方、スケールフリー性と階層構造はその医療知識の生成メカニズムと関係していると考えられる。医療の知識は常に変化している。病名の追加、定義の変化、新しい知識の追加、古い知識の削除などが行われる。新しい知識はMKNにおける新しい頂点の追加に対応する。新しく追加された頂点はすでにある頂点と枝で繋がれる。その接続において優先選択原理が働く可能性は十分考えられる。また、医学の知識は複雑な階層構造を持っている。新しくnodeを追加する場合に旧来の階層構造を保ちながら成長する必要がある。このような二つの原理が働いて医療知識のネットワークが成長していくものと考えられる。
医療知識ネットワークは単に知識上のネットワークなのであろうか。それとも実際の医療者の医療行動と関係があるのであろうか。医療知識ネットワークが単なる医療テキストが示す構造を示しているならば、実際の医療における利用、応用は限られる。しかし、もし、このネットワーク構造が医療者の医療行動に影響するならばその意味することは重大である。それを調べるため、医師の行動を反映していると思われる病院情報システム内の病名データベースを利用した。病名データベースは医師の日常の診療において、診察している患者の病名をその都度、コンピュータに入力することにより作られたデータベースである。データベース内の病名は必ずしも確定診断を意味するものではない。患者の推定病名は診療や検査を行うにしたがって変化する場合もある。そのような場合には同じ患者に対して何種類もの病名が登録されていく。すなわち、患者の診察行動に従って登録される病名は変化していくのである。このデータベース内の一つの病名に関しては、患者番号、科コード、病名コード(ICDコード)、医師コード、入力日、入力端末コードなどの情報が同時に記録される。これらの情報を単純にネットワーの頂点とし、同じレコード内の頂点同士を枝で繋ぐことによって病名データベースネットワーク(the Diagnosis Database Network: DDN)を構成することができる。
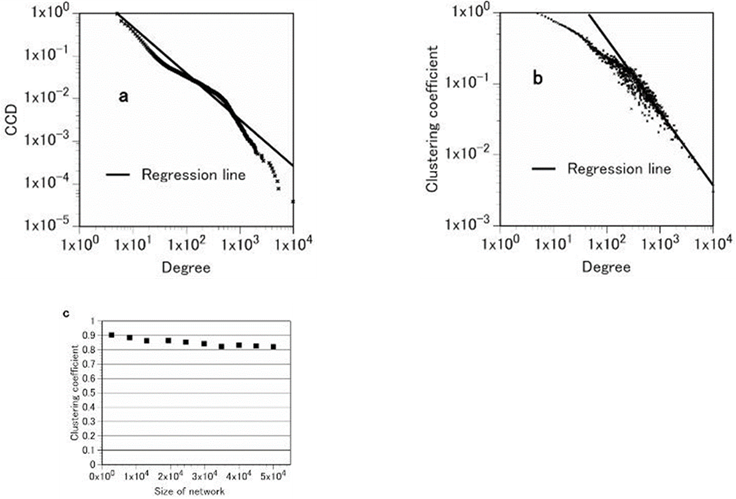
a.DDNの次数の相補累積分布(CCD)
b.次数\(k\)のnodesの平均クラスタ係数(\(C(k)\))
c.ネットワークサイズ毎の平均クラスタ係数
文献[98][99]
表Ⅲ-4-3に示すようにDDNはスモールワールドの性質を示す。さらに、DDNはMKNと同様にスケールフリーで階層構造を持つネットワークであることが示された(図Ⅲ-4-9)。しかも、MKNの平均クラスター係数は0.86、次数分布のベキ指数は2.045であり、DDNのそれらはそれぞれ0.83と2.084といずれも非常に近い値である。これらの事実はDDNがMKNと非常に似たネットワーク構造を持っていることを示唆する。
医師の病名付けという行為のネットワークを表しているDDNと医学知識のネットワークが非常に似通った性質を持っていることは驚くべき事実である。この事実から次のような可能性を考えることができる。
- 1)医師の医療行為を行うための頭の中の知識構造自体がMKNと似通っている。
- 2)その知識構造を利用して病名診断がなされる。
- 3)知識構造のスモールワールド性によって、膨大な医学知識を使いこなすことができる。
- 4)結果としての病名同士がある種の関係(ネットワーク的結びつき)を持っている。
- 5)医師の医療行為が一般的医学の知識構造に影響を与える。
医師の行動とMKNの関係を調べるために、医師の意思決定行動をMKN上の粒子の動きにたとえてみよう。
MKNにおいて、任意の頂点からネットワーク上をランダムに動く粒子を考える。この粒子が最初に訪問した病名が医師の診断であるとする。この操作を何度も繰り返すと、病名の頻度分布が得られる。こうして得られた病名の頻度は各病名の次数に比例するであろう。そこで、MKNにおける病名(診断名)の頂点の次数分布を調べてみる。
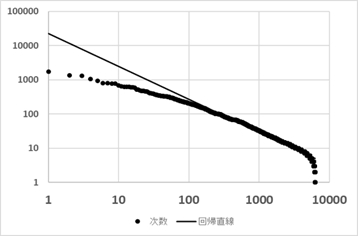
Zipf指数 \(\zeta\ = 0.96\)
文献[98][99]
図Ⅲ-4-10はMKNから病名の頂点を取り出してその次数を順にならべた図(Zipfプロット)である。図から分かるようにZipfプロットにおいてベキ法則が成り立っていることがわかる。またそのZipf指数 \(\zeta\) は0.96であるので、ベキ指数 \(\alpha\) は2.04となる(付録Ⅲ-4)。第4章の1節でも述べたように病院における病名頻度もベキ法則が成り立つ。しかも、そのZipf指数は表Ⅲ-4-1に示したように1前後(ベキ指数では2前後)である。MKNの次数分布のZipf指数とよく似ている。実際の病名頻度とMKNの病名の次数が同じようなベキ法則に従うことは非常に示唆的である。知識ネットワークにおいて次数が大きいということはそのtermがより沢山参照されることを示している。次数が大きいということは多くの語と繋がっているということであり、それだけ、よく使われ、選ばれる可能性がある。このような理由で今回の結果が得られたと考えられる。このことは文章の単語頻度と文章から作ったネットワークの次数分布が強く相関するという事実とよく似ている。しかし、文章の場合はその文章内の単語の頻度であるが、今回の結果は文章内の病名の出現頻度ではなく、実際の診療における病名頻度であり意味するところは少し異なっているし、より重要な結果であると考えられる。
このように実際の病名頻度分布と医療知識ネットワークの次数分布が似ているのはなぜであろうか。その可能性として次のようなことが考えられる。
- 1)テキストは常に実際の医療の中での病気の新しい知識を反映する。 すなわち、医療の中でよく出現する病気はテキストでもその影響を受けて沢山記述される。
- 2)テキストに良く出現する病気は医師が連想しやすい。
- 3)診断する医師の頭の中の知識構造はテキストが示す知識構造とよく似たネットワーク構造を持っている。
- 4)逆にテキスト自体が常に現場の医師の医療行為の影響を受けて変化している。
5.医療は複雑系である
第3章とこの章において、医療の中に出てくる多くの複雑系的な性質を述べた。特に複雑系でよくみられるベキ分布について医療の中での現状を述べた。第3章でも述べたように、医療に出現するベキ分布は大きく3つの種類に分けられる。一つ目は病名の頻度や手術術式の頻度のような「カテゴリーの頻度分布」である。二つ目は手術中の出血量の分布のような「量の分布」である。そして、三番目が入院日数、手術時間、病気の回復までの期間のような「時間分布」に関するものである。
これらのうち、後の二つについては3章-4においてその成因を考えた。三番目の入院日数については、ランダムウォークが最も重要な因子である。これは、患者の状態がランダムに変動するという考えである。ランダムに変動する原因については、複雑系的には生体の各種臓器の相互作用が全体として患者の平均的状態をランダムに揺り動かしているのであると解釈できる。二番目の出血量については、その重要な因子は血管のフラクタル性である。複雑系的にみれば、人体の発生過程における組織、細胞間の複雑な相互作用によって、血管走行がフラクタルになっていると考えることができる。このように考えると、二番目の「量の分布」と三番目の「時間分布」におけるベキ分布は第3章-1で述べた生体におけるカオスと同様、個々の生体内の複雑性の反映であるとみることができる。それに対して、この章で述べた病名などの「カテゴリーの分布」に現れるベキ分布は個別の生体内の複雑性ではなく、医療という「社会構造の複雑性」の反映であると考えられる。
第4章-3においては医学教科書から作ったネットワークを分析した。その結果、MKNはスモールワールドでスケールフリーかつ階層性を示した。さらに、実際の医療行為を反映していると考えられる病名データベースが同じ構造をなすことを示した。このように、MKNが実際の医療行為を反映していることはMKNを調べることの重要性を示している。さらに、このような事実は医療というもの自体が複雑系を成していることを示していると考えられる。そのことを考えるために複雑系の定義を再掲しておこう(第2章参照)。
- 1)システムは多数の要素(エージェント)によって構成される。
- 2)各エージェントは互いに局所的な相互作用を行う。
- 3)この局所的な相互作用によって各エージェントの性質からは予測できない全体の性質・状態・振る舞いが出現する。
- 4)この全体的な性質・状態・振る舞いが個々のエージェントの振る舞いに影響を与え、個々のエージェントの振る舞いが変化する。
この定義をみて、我々は漠然と生物集団、人間の社会集団などが複雑系であろうと考える。それはその通りである。しかし、人間社会と生物集団の大きな違いは人間には言葉があるということである。生物集団をコントロールする情報は身振り、目の動きなど行動である。行動は時間空間的に局所的な影響しか与えることはできない。そのため、生物集団はまさに、上記の2)に示した局所的な相互作用を営む集団である。しかし、言語は時間的にも空間的にも遠い世界へ影響を与えることができる。その意味では、人間社会は互いに局所的な相互作用だけを営んでいるわけではない。政治的集団、社会活動の集団、会社組織などは言語という大域的な影響を与える方法(規則、法律)によってまとまっている。もちろん、個々の構成員同士はそのような大域的影響だけではなく、局所的な影響による相互作用も行っている。そのため、その相互作用によって集団自体の方向が変化し、集団の規則に反する動きをすることもある。この点では正に複雑系的影響が起こっていると考えられる。
人間社会を規定する大域的な規則(言語)は、法律などを考えれば分かるように厳密に定義された言語に近い。言い換えれば、数学的な言語である。前述したように、数学的言語の特徴は厳密な定義から始まりそこから演繹した論理で作られていることである。昔はともかく、現代の社会を規定する言語はこのようなタイプに進化していると思われる。例えば、工場生産を見てみよう。工場においてはまず、その製品が厳密に定義される。設計図に始まり、内容成分まで規定した材料表などは正にそのようなものである。さらに、生産工程そのものも定義されている。以前はいわゆる匠の技という方法で生産されているものも多かったが、現在ではそれらの技は精密にマニュアル化され誰が行っても同じ製品が出来るようになりつつある。その傾向はますます強くなり、工場生産以外の世界にも広がりつつある。飲食店などの業界は、最近まで匠の技の世界であった。また、接客も「お客の心をうまくつかむ」という匠の技が用いられていた。しかし、アメリカから世界に広がったファーストフードの世界は、この食品業界にマニュアルという工程表を導入した。客が来たときに話す内容、商品の勧め方などに関して、非常に細かい行動マニュアルが作られている。このようなマニュアル化によって、従業員の行動は規定されてしまい、客との局所的な自由な相互作用は失われつつある。
医学の世界でも同様の試みが進みつつある。DRG/PPS(日本ではDPC)はそのような試みの代表である。患者群をDRGというコードによって分類し、同じ分類に対して同じ医療行為(クリニカルパス、略してパスと呼ばれる)をしようという試みである。このことによって、医療行為のマニュアル化が進んでいる。医師による患者毎の個別の対応は徐々に失われ、どの医師がやっても同じ結果を生むことを理想とするようになってきた。ある学会で、演者が「今や、患者に行う行為において、ワクワク、ドキドキは必要ない。決まったことを決まった手順で淡々と行う時代である。」と述べていた。もはや、名医は必要ないし、どの医者がやっても同じであるというのが理想になりつつある。
このような方法はどんどん進んでいる。しかし、いまだにクリニカルパスから外れる患者は多数いる。各病院ではクリニカルパスから外れる患者をバリアンス(variance)と呼び、それが出た場合にはその患者にも適応できるようにクリニカルパスの修正を行う。現在、パスから外れるのは、パスがまだ不完全なためであり、修正を繰り返せば、いずれは全ての患者をパスによって治療できると考えている。しかし、このことは本当なのであろうか。もしかしたら、クリニカルパスから外れる患者は如何にクリニカルパスを修正しても減らないのかもしれない。第3章-3で述べたように、異常値は稀ではないという現象が起こっているのかもしれない。
言語というのは、元々情報の縮約という機能を持っている。人間は全ての犬を一括して「イヌ」という同じ名前で呼んでいる。犬は一体世界で何匹いるのであろうか? それをすべて「イヌ」という一つの言葉で代表させている。この機能によって、世界を単純に考えることができる。もし、言葉にこの機能が無ければ、個々の犬を別々の言葉で呼ばなければならない。そうすれば、世界はずいぶん複雑である。もちろん、これは言語だけの機能であるとは言えない。言葉を持たない動物も動物の種類を分かっている可能性はある。実際ペットの犬は明らかに犬と猫を区別している。「犬同士は犬であると認識しているし、猫は別である」と思っているようである。しかし、この認識を一つの記号であらわすのと、単純に認識しているという事実とは別の問題である。言語という記号で表すことにより実際に犬が存在しない状態でも、犬について考えたり、ほかの人と犬について論ずることができる。ともかく、人間は言葉により非常に多様な世界を少ない記号で表現し伝達することが出来るようになったのである。
言語はこのように、世界をより小さな情報で表す機能を持っている。しかし、言語によってあらわされた世界と実際の世界は異なっている。そのため、問題を起こす。犬を一括して「イヌ」と表現しても、時にはある犬と他の犬を区別する必要が出てくる。ある犬は人懐っこくてかんだりしない。しかし、他の犬は人間に攻撃的である。そうすると、この二つを区別する必要が出てくる。そのため、この二つを区別するために新しい言葉を想像する必要がある。このような作業は言語で実際の世界を表現しようとすれば必然的に起こってくる。次々と新しい言葉を創造し、いらなくなった言葉を削除し、時には言葉の意味を変更する。このような絶え間ない変更によって作られ続けるのが言語である。その意味では、言語自体が複雑系であると考えることができる。このように、世界の変化、人間の変化に合わせながら常に変化していくのが本来の「ことば」である。
しかし、そのような中で、変化しないものを表すような言語も生まれてきた。数学がその典型である。数学は言語であるがその対象、すなわちそれが表すものは変化しない。というか、変化しないものを創造してそれを表現するのが数学である。直線や三角形は、概念であり、本当の世界には存在しないものである。数学の構造は定義から始まる。まず、直線を定義して、そのあとで、その定義に従ってその性質を論じ、表現する。定義するとは、創造することである。もともとの「ことば」はすでにあるものを表現することから始まったと考えられる。しかし、数学の場合には存在するのではなく、創造するのである。創造するのであるから、その性質が途中で変化することはない。これは、実際に存在する物を表現する場合にはありえないことであるが、創造した場合にはあり得る。
人間社会は、「ことば」によって表現するだけではなく、数学のように創造する社会でもある。昔から、植物を作り、家を作り、馬車を作り、町をつくり、国を作ってきた。このように作る世界にとっては、数学という言語は非常に有利であったのであろう。数学的な世界は途中で言葉の意味が変わったりはしない。最初に決めた定義通りに動いていく。この流れが、産業の定型化、マニュアル化を生み出してきたともいえるであろう。
さて、医療の話に戻ろう。前述したように、医療も定型化、マニュアル化を進めてきた。しかし、必ずしもうまくいかない。その原因は医療の複雑性にあることをこの本で論じてきた。では、なぜ医療は他の産業などと異なりいつまでも複雑性を保っているのであろうか。一言で言ってしまえば、医療は作られた制度というより、病気を表現する制度であるからである。西洋医学においては、病気というものを病名という名で分類した。これは犬に「イヌ」と名付ける行為と同じである。もともと、病名により病気を認識し、病名毎の対応をしようとしたのが西洋医学である。しかし、実際にある病気を正確に表現することは出来ない。そのため本来の「ことば」と同じ現象が医療において起こったのである。医療は常に対象の影響を受ける。痛みのところで述べたように、如何に痛みを医学的に定義しようと患者の痛みの性質が合わなくなれば、定義を変えざるを得ない。対象自体、人間が作ったものではなく、元々あるものである。そのために、その性質を数学のように定義することはできない。対象が変化すればそれに合わせて医学自体も変化せざるを得ないのである。このような変化を記述してくことにより医学書も出来上がっている。このような変化の集積が医学書であり、その結果MKNが複雑系の性質を持つことになったと考えられる。MKNの複雑系的性質は、医療そのものの複雑性を表している。医療は一見、自動車産業などと同じように、人間が作った制度に見える。しかし、本質的にはきっちり規定することができない複雑系であると思われる。このことを認識しなければ、医療問題を解決できないのかもしれない。もしくは、医療問題は本質的に解決できない対象なのかもしれない。医療問題は解決するのではなく継続的に解決努力をしなければならない対象なのであろう。
脚注
- ただし、現実には最近までほとんど線形の積み上げが行われていた。 ↩︎
- 実数から実数への関数の場合は、二つも式はいらない。どちらか一つで十分である。複素数から複素数への関数やベクトルからベクトルへの関数の場合はこれら二つの定義式が必要である。 ↩︎
- \(y=ax+b\) は厳密には線形関係ではないことになるが、原点をずらせば \(y=ax\) になるので、一般には線形関係と考えている。
\(y=ax\)は一つの変量 \(x\) と一つの変量 \(y\) との関係であるが、二つの数の組 \((x,y)\) と \((x’,y’)\) が
\begin{eqnarray}
\left\{
\begin{array}{l}
x’=ax+by \\
y’=cx+dy
\end{array}
\right.
\end{eqnarray}なる関係で結ばれているときにも、\((x,y)\)と\((x’,y’)\)は線形関係にあると呼んでいる(これはベクトルからベクトルへの線形関係である)。さらに、3つの数の組、4つの数の組と増えても同様である。 ↩︎ - これらの式は時間がとびとび(月毎)であるが、時間を連続にすると微分方程式と呼ばれる式になる。 ↩︎
- ただし、線形相互作用をしている系の時間変化を表す関数は決まっている。定数、線形関数、三角関数(\(sin\)もしくは\(cos\))、指数関数とこれらの和からなる関数のみが出てくる。 ↩︎
- このような方法が統計学でいうところの線形回帰法である。一般の多変量解析法はすべて線形近似の方法である。 ↩︎
- このような現象を内的観測と呼んでいる。 ↩︎
- 変化方程式には前に述べたように、時間が連続な場合の微分方程式と時間を離散的(1,2,3、…)に扱うものがある。時間が離散的である場合は、時間を整数\(n\)で表して
\(x_{n+1}=f({x_n})\) という形の方程式を扱う。このような方程式は高校数学ではいわゆる漸化式である。また、回帰式とも呼ばれる。これはxn+1を求めようとすると
\(x_{n+1}=f(x_n)=f(f(x_{n-1})=f(f(f(x_{n-2})))=…=f(f(f(f…(f(x_0)))..)\)と自己回帰的に戻っていくからである。また、コンピュータプログラムの世界ではこのような関係を再帰呼び出しとか再帰関数と呼んでいる。 ↩︎ - 少しというのは、大きく動かすと戻ってこないこともあるという意味である。非線形方程式では安定な状態は複数あることが多く、大きく動かすと他の安定な状態に引き込まれる。 ↩︎
- フラクタルについては、参考文献を参照してもらいたい。 ↩︎
- システムとは今考えている対象の全体である。客観的に存在するというよりは観察者の恣意性が決めている。 ↩︎
- エージェントといっても、必ずしも人間のような意思を持つ個体と考える必要はない。組織でも生物の臓器でも概念でもよい。これも観察者によって一まとまりと考えられるものなら何でもよい。 ↩︎
- 確率変数というのは事象から実数への写像という意味である。身長の例でいえば、事象というのは各個人、実数というのは身長を表す。例えばある個人を \(\omega\) であらわすと、\(X(\omega)=152\) とは個人 \(\omega\) の身長が152cmであることを表している。 ↩︎
- \(Pr\)(\(X \)の式) とは \(X \) がこの式を満たす確率という意味。\(Pr(X \leq x)\) というのは、正確には \(Pr\{\omega \mid X(\omega) \leq x \}\) という意味で、身長が \(x\) 以下である個人 \(\omega\) の集合の確率という意味である。確率というのは \(\omega\) の集合の全体に対する割合のことである。 ↩︎
- もっと正確に求めるには [18] ↩︎
- ここで \(\alpha_i\) が定数だとすると、\(X_i\) は指数関数的に増加あるいは減少する。しかし、細胞内の化学反応では、\(\alpha_i\) は周りの環境によってゆらいでおり、一定ではないと考えられる。 ↩︎
- ここは、「複雑系のカオス的シナリオ」[2]を参照にすること。 ↩︎
- 時間とともに変化するデータ。 ↩︎
- パワースペクトルは時系列データをフーリエ変換して行う。フーリエ変換はプログラムによって行うが、最も頻用されるプログラムはFFT(Fast Fourier transform)と呼ばれるもの。 ↩︎
- 正確には多くの病名頻度は完全なベキ分布から少しずれた分布をする。正確には2章-2で説明する「切り捨てベキ分布」であると考えられる。 ↩︎
- ここでの平均入院日数は退院患者の実際の入院日数を平均したものである。厚生労働省が指定する平均在院日数とは計算方法が違う。 ↩︎
- 現在はMEDS-DCという組織から標準病名マスターが提供されている。そのため、ここでの議論はすでに当てはまらないかもしれない。以下の議論の内容をオーダリング内の新しい病名の増加と読み替えてもらいたい。ただ、各病院では起こらないかもしれないが、標準病名マスターの作成時には同じ問題が起こり、標準病名マスターの更新をいつまでもし続ける必要があるかもしれない。 ↩︎
- 必要病名数は理論的に計算できる(図Ⅲ-3-13)。計算式は付録Ⅲ-5参照。 ↩︎
- ベキ分布をする場合の平均値は次のように計算する。
\begin{eqnarray}
平均値= \frac{\displaystyle\sum_{n=1}^{\infty}n \frac{A}{n^{\alpha}}}{\displaystyle\sum_{n=1}^{\infty} \frac{A}{n^{\alpha}}} \approx \frac{\displaystyle\int_1^{\infty}X \frac{A}{X^{\alpha}}}{\displaystyle\int_1^{\infty} \frac{A}{X^{\alpha}}}
\end{eqnarray}
この式は \(\alpha \leqq 2\) ならば \(\infty\) になる。分散も同様に計算できる。 ↩︎ - 図Ⅲ-3-9で横軸を入院日数、縦軸をその入院日数の人数と読み替える。 ↩︎
- 指数分布とは \(Y=Ae^{-aX}\) の式で表される分布。この節で論じている分布の性質としては正規分布と同様である。 ↩︎
- 平均値に限らず中央値など他の統計指標も同様に使えない。 ↩︎
- \(f(n) \approx g(n)\) (漸近的に等しい)とは \(\frac{f(n)}{g(n)} \xrightarrow[n \to \infty]{}c \ (0 \lt c \lt 1)\) となる時である。 ↩︎
- 正確に言うと、左右ではなくそのままの位置か右 \((x+1)\) である。なぜ、「左に流れないか」というと、左に流すと隣の水源の水が右に流れると交差するからである。 ↩︎
- International Stastistical Classification of Diseases and Related Health Problems [65] ↩︎
- ただし、図の(A)、(B)とは異なった時期のデータである。 ↩︎
- すでに何度も述べているように、ベキ指数 \(\alpha\) とZipf指数 \(\zeta\) の関係は、\(\alpha = (\zeta +1)/\zeta\) ↩︎
- 例えば、胃がんという病名は胃癌、胃がん、胃ガンなどと異なって表現される。 ↩︎
- オピオイドの作用は中枢作用以外にも多くの作用がある。 ↩︎
- aは相補累積分布。回帰直線の傾きから、\(\beta =1.04417\) である。次数分布のベキ指数は \(\alpha = \beta +1 =2.045\) である(付録4参照)。 ↩︎
- 連続と言うのは飛び飛びではなくつながっているという意味だが、具体的には時間が飛び飛びの数(自然数や整数)ではなく実数(小数)で表されるという意味。 ↩︎
- \(n(i, j, k\) なども) は一般に整数や自然数をあらわすときに使う。\(t(x, y, z\) なども) などは実数を表すときに使う。また、\(x_n\) と書いても \(x(n)\) とかいても同じ意味になるが。ふつう \(x_n\) と書くときは \(n\) が整数であるという暗黙の了解がある(数列をイメージする)。\(x(t)\) と書くと普通は \(t\) が実数であるというイメージがある。いずれにしてもこれらは習慣であるので、どちらを書いても間違いではないが、普通は習慣に従うほうが間違えにくい。 ↩︎
- \(dx\) の \(d\) というのは差(difference)という意味の記号である。\(d\) と \(x\) を掛けたものでは無い。何の差かというと、\(t+h\) のときの\(x\)と\(t\) の時の \(x\) の差 \(x(t+h)-x(t)\) を表す。厳密にはちょっと違うが、こんな理解で充分である。\(dt\) というのは変であるが、\(t+h-t\) という意味であり、結局は\(h\)となる。 ↩︎
- 右辺の形によっては解けないこともあるが、大概は解ける。 ↩︎
- 実際のコンピュータでの計算法は、ここで示した方法と少し異なっている。ここでやったような方法は \(h\) が非常に小さい場合はほぼ正しいが、すこし大きくなると誤差が大きくなる。そのため、コンピュータでの計算では誤差を小さくするような工夫がなされている(ルンゲクッター法)。 ↩︎
- 確率変数というのは、ある事象に関して、起こりうる事柄に割り当てている値をとる変数という意味。例えば、サイコロの場合は取りうる値は \(1, 2, \cdots , 6\) の6種類をとる。この6種類をとる変数を \(X\) とすると、\(Pr(X=6)\) とは値6を取る確率 \((1/6)\) という意味。\(Pr(X \geq 4)\) は4以上(\(4,5,6\))を取る確率(\(1/2\))という意味である。 ↩︎
参考文献
[1] 金子邦彦、池上高志、津田一郎「複雑系の進化的シナリオ―生命の発展様式(複雑系双書)」朝倉書店 1998
[2] 金子邦彦、津田一郎「複雑系のカオス的シナリオ(複雑系双書)」 朝倉書店 1996
[3] 合原一幸 編「カオス時系列解析の基礎と応用」 産業図書 2000
[4] フェダー J フラクタル 啓学出版 1991
[5] マンデブロ B フラクタル幾何学 日経サイエンス社 1985
[6] 安富 歩「貨幣の複雑性」 創文社 2000
[7] Bak P, How Nature Works: The Science of Self-Organized Criticality, New York: Copernicus. ISBN 0-387-94791-4, 1996.
[8] グルーグマン P「自己組織化の経済学」東洋経済新報社 1997
[9] 高安秀樹、高安美佐子「経済・情報・生命の臨界ゆらぎ―複雑系科学で近未来を読む」ダイヤモンド社 2000
[10] 高安秀樹「経済物理学(エコノフィジックス)の発見(光文社新書)」 光文社 2004
[11] 増田直紀、今野紀雄「複雑ネットワーク:基礎から応用まで」近代科学社 2010
[12] Mandelbrot BB, The stable Paretian income distribution when the apparent exponent is near zero, Int. Econ. Rev. (1963) 4, 111-115.
[13] Mantegna RN, Buldyrev SV, Goldberger AL, Linguistic features of noncoding DNA sequences, Phys. Rev. Lett. (1994) 73, 3169-3172.
[14] Nicolis JS, Tsuda I, On the Parallel between Zipf’s Law and 1/f Processes in Chaotic Systems Possessing Coexisting Attractors, Prog. Theor. Phys. (1989) 82, 254-274.
[15] Okuyama K, Takayasu M, Takayasu H, Zipf’s law in income distribution of companies, Pyhsica A (1999) 269, 125-131.
[16] Sato A, Takayasu H, Dynamic numerical models of stock market price: from microscopic determinism to macroscopic randomness, Physica A (1998) 250, 231-252.
[17] Zipf GK, Human Behavior and the Principle of Least Effort, Cambridge Mass, Addison-Wiesley, 1949.
[18] Clauset A, Shalizi CR, Newman MEJ, Power-law distributions in empirical data, SIAM Rev. 51 (2009), 661-703.
[19] Newman MEJ, Power laws, Pareto distributions and Zipf’s law, Contemporary Physics (2005) 46, 323-351.
[20] フェラー W「確率論とその応用Ⅰ (上)(下)」紀伊国屋書店 1960
[21] Bak P, Tang C, Wisenfeld K, Self-organized criticality, Phys. Rev. A. (1988)38, 364-374.
[22] 河合泰男、鈴木理「集団遺伝学における折れ棒モデル」数理解析研究所講研録 2008 1597 209-213
[23] 時田恵一郎、入江治行「島の生物地理学とZipf の法則」数理解析研究所講研録 2006 1499 1-6
[24] 高山学「入院日数の分布モデル」日本保険医学会誌 2010 108(2) 120-134
[25] 赤澤宏平, 柳川堯 サバイバルデータの解析 バイオ統計シリーズ③ 近代科学社 2010
[26] 金子邦彦「生命とは何か」東京大学出版会 2019
[27] 國仲寛人、小林奈央樹、松下貢 複雑系にひそむ規則性―対数正規分布を軸として- 日本物理学会誌(2011) 66(9)、658-665
[28] Sano M, Sawada Y, Measurement of the Lyapunov Spectrum from a Chaotic Time Series. Phys. Rev. Lett. (1985), 55(10), 1082-1085.
[29] Wolf A, Swift JB, Swinney HL, Vastano A, DETERMINING LYAPUNOV EXPONENTS FROM A TIME SERIES. Physica D (1985), 14, 285-317.
[30] Kilborn KM, Barger AC, Shannon DC, Cohen RJ, Benson H, Assessment of autonomic function in humans by heart rate spectral analysis. Am J Physiol. (1985) 248, H151-H153.
[31] Goldberger AL, Rigney DR, Mietus J, Antman EM, Greenwald S, Nonlinear dynamics in sudden cardiac death syndrome: Heartrate oscillations and bifurcations. Experientia(1988), 44(11-12), 983-7.
[32] Eckmann JP, Kamphorst SO, Liapunov exponents from time series, Phys. Rev. A. (1986), 34(6), 4971-4979.
[33] Tsuda I, Tahara T, Iwanaga H, CHAOTIC PULSATION IN HUMAN CAPILLARY VESSELS AND ITS DEPENDENCE ON MENTAL AND PHYSICAL CONDITIONS. International Journal of Bifurcation and Chaos(1992), 2(2), 313-324.
[34] 津田一郎、田原孝、岩永浩明 指尖脈波のカオスとその情報論的意味 Holonics(1992), 3, 163-176.
[35] 田原孝 臨床におけるカオスの応用 バイオメカニズム学会誌(1995), 19(2), 105-116.
[36] Sumida T, Tahara H, Iwanage H, A physiological significance of Shilnikov phenomenon in the focal accommodation systems of human eyese. Int. J. Bifurcation and Chaos(1994), 4(1), 231-236.
[37] Babloyantz A, Evidence of Chaotic Dynamics of Brain Activity During the Sleep Cycle. Physics Letters A(1985), 111(3), 152-156.
[38] 「データベース構築促進及び技術開発に関する報告書」財団法人データベース振興センター 1989
[39] 「データベース構築促進及び技術開発に関する報告書-意味情報を中核とした医療評価データベースとコミュニケーションシステムの構築-」財団法人データベース振興センター 1990
[40] 「データベース構築促進及び技術開発に関する報告書-健康の自己管理と病気予防データベースの構築-」財団法人データベース振興センター 1991
[41] Imanishi A, Oyama-Higa M, The Relation between Observers’ Psychophysiological Conditions and Human Errors during Monitoring Task. 2006 IEEE Conference on Systems, Man, and Cybernetics(2006), 2035-2039.
[42] Oyama-Higa M, Miao T, Mizuno-Matsumoto Y, Analysis of dementia in aged subjects through chaos analysis of fingertip pulse waves. 2006 IEEE Conference on Systems, Man, and Cybernetics(2006), 2386-2867.
[43] 藤田悦則,小倉由美,落合直輝, 苗鉄軍, 清水俊行, 亀井勉, 村田幸治, 上野義雪, 金子成彦 指尖容積脈波情報を用いた入眠予兆現象計測法の開発 人間工学(2005) 41(4), 203-21.
[44] 山添守史、串田淳一、亀井且有「Emotional Fitness のための加速度脈波を用いた運動後爽快感指標の提案」26th Fuzzy System Symposium (2010), 217-22.
[45] 石山さゆり、岩永浩明、田原孝、清岡佳子、大橋一友「胎児と母は決定論的カオスである- サロゲート法による解析-」看護理工学会誌 2018, 5(1), 74-79.
[46] Ishiyama, S., Iwanaga, H., Tahara, T., Kiyooka, Y., & Ohashi, K. Fetus and mother are a deterministic chaos-Analysis of surrogate data method-. The Society for Nursing Sci. and Eng. 5(1), 74-79(2018).
[47] Ishiyama, S., Tahara, T., Iwanaga, H., Kiyooka, Y. & Ohashi, K. Emotional Changes in Fetuses and Mothers over the Course of Pregnancy: Chaos Analysis of Heart Sounds, Int. J. caring sci. 13(3), 1545-1554(2020).
[48] Fink W, Lipatov V, Konitzer M, Diagnoses by general practitioners: Accuracy and reliability, International Journal of Forecasting (2009) 25, 784-793.
[49] Tachimori Y, Tahara T, Clinical Diagnoses Following Zipf’s Law, Fractals (2002) 10, 341-351.
[50] 田原孝、日月裕「実践から病院情報システムの功罪とそのあり方を考える 今後のあるべき医療情報システム カオス・複雑系医療への序章(その1)」 病院(2001) 60 (2) , 128-134.
[51] 田原孝、日月裕「実践から病院情報システムの功罪とそのあり方を考える 今後のあるべき医療情報システム カオス・複雑系医療への序章(その2)」 病院(2001) 60 (3), 233-239
[52] 川渕幸一「DRG/PPSの全貌と問題点」薬事時報社 1997
[53] MORIYAMA O, ITOH H, MATSUSHITA S, MATSUSHITA M, Long-Tailed Duration Distributions for Disability in Aged People. J. Phys. Soc. Jpn. (2003) 72(10), 2409-2412.
[54] Whitmore GA, Neufeldt AH, An application of statistical models in mental health research, Bulletin of Mathematical Biophysics (1970) 32, 563-579.
[55] Whitmore GA, The Inverse Gaussian Distribution as a Model of Hospital Stay, Health Serv Res (1975) 10(3), 297–302.
[56] 胡内誠、日月裕、星雅丈 急性期病院と療養・介護型病院における入院期間分布の違い 医療情報学 (2005) 25 (Suppl.), 245-248.
[57] Barry R, FRACTAL ANALYSIS OF THE VASCULAR TREE IN THE HUMAN RETINA, Annu. Rev. Biomed. Eng.(2004) 6, 427–52.
[58] Cohen R, Havlin S, Scale-Free Networks are Ultrasmall, Phys. Rev. Lett. 90 (2003), 058701.
[59] Johannes HGM, James BB, Stephen AR, FRACTAL NETWORKS EXPLAIN REGIONAL MYOCARDIAL FLOW HETEROGENEITY, Adv Exp Med Biol. (1989) 248, 249–257.
[60] 松尾崇「生体のフラクタル構造」バイオメカニズム学会誌 1995 19(2), 125-131.
[61] 松尾崇、大野京子「眼底血管像のフラクタル次元」MEDICAL IMAGING TECHNOLOGY(1997) 15(5), 592-596.
[62] Takayasu H., Nishikawa I, Tasaki H, Power-law mass distribution of aggregation system with injection. Phys. Rev. A (1988) 37, 3110-3117.
[63] Rodríguez-Iturbe I, Ijjasz-Vasquez E, Bras RL, Tarboton DG, Pwer-law distributions of mass and energy in river basins, Water Resour. Res.(1992) 28(4), 1089-1093.
[64] Family F, Masters BR, Patt DE, FRACTAL PATTERN FORMATION IN HUMAN RETINAL VESSELS, Physica D.(1989) 38, 98-103.
[65] 厚生省大臣官房統計情報部編「疾病、傷病および死因統計分類提要 ICD-10 準拠 第1 巻~第3巻」1995
[66] Barrat A, Barthélemy M, Vespignani A, Dynamical Processes on Complex Networks, Cambridge University Press, Cambridge, 2008.
[67] Bollobás B, Random Graphs (Second Editon), Cambridge University Press (2001).
[68] Newman MEJ, Networks An Introduction, Oxford University Press, Oxford, New York, 2010.
[69] 今野紀雄、井出雄介 複雑ネットワーク入門 講談社サイエンティフィック 2008
[70] Bollobás B, Riordan O, The diameter of a scale-free random graph, Combinatorica, 24 (2004), 5-34.
[71] Bollobás B, The Diameter of Random Graph, Trans. Amer. Math. Soc. 267 (1981b), 41-52.
[72] Erdös P, Rényi A, On random graphs, Publ. Math. 6 (1959), 290-297.
[73] Erdös P, Rényi A, On The Evolution of Random Graphs, Publ. Math. Inst. Hunga. Acad. Sci. 5 (1960), 17–61.
[74] Gilbert EN, Random Graphs, The Annals of Mathematical Statistics (1959) 30(4), 1141—1144.
[75] Chung F, Lu L, The Diameter of Random Sparse Graphs, Advances in Applied Mathematics 26 (2001), 257–279.
[76] Klee V, Larman D, Diameters of Random Graph, Can. J. Math. 33(3) (1981), 618-640.
[77] Newman MEJ, Random graphs as models of networks, arXiv:cond-mat/0202208[cond-mat.stat-mech].
[78] Watts DJ, Strogatz SH, Collective dynamics of ‘small-world’ networks, Nature (1998) 393, 440-442.
[79] Amaral LAN, Scala Barthélémy AM, Stanley HE, Classes of small- world networks, PNAS 97 (2000) 11149-11152.
[80] Milgram S, The Small-world problem. Psychology Today (1967) 1(1), 61-67.
[81] Travers J, Milgram S, An Experimental Study of the small World Problem. Sociometry (1969) 32(4), 425-443.
[82] Barabási AL, Albert R, Emergence of scaling in random networks, Science(1999) 286, 509-512.
[83] Barabási AL, Ravasz E, Vicsek T, Deterministic scale-free networks, Physica A (2001) 299, 559–564.
[84] Barabási AL, Albert R, Jeong H, Mean-field theory for scale-free random networks, Physica A 272 (1999), 173-187.
[85] Albert R, Jeoung H, Barabási AL, Diameter of the World Wide Web, Nature 401 (1999) 130-131.
[86] Dorogovtsev SN, Goltsev AV, Mendes JF, Pseudofractal scale-free web, Phys. Rev. E (2002) 65, 066122.
[87] Dorogovtsev SN, Mendes JFF, Evolution of reference networks with aging, Phys. Rev. E(2000) 62, 1842.
[88] Jeong H, Tombor B, Albert R, Oltvai ZN, Barabási AL, The large-scale organization of metabolic networks, Nature (2000) 407, 651-654.
[89] Ravasz E, Barabási AL, Hierarchical organization in complex networks, Phys. Rev. E (2003) 67, 026112.
[90] Ravasz E, Somera AL, Mongru DA, Oltvai ZN, Barabási AL, Hierarchical organization of modularity in metabolic networks, Science (2002) 297, 1551-1555.
[91] Lee J, Park NK, Scale-free Networks in the Presence of Constraints: An Empirical Investigation of the Airline Route Network, Seoul Journal of Business (2007) 13(1), 3-19.
[92] Maschberger, Kroupa TP, Estimators for the exponent and upper limit, and goodness-of-fit tests for (truncated) power-law distributions, Mon. Not. R. Astron. Soc. (2009) 395, 931-942.
[93] Mossa S, Barthélémy M, Stanley HE, Amaral LAN, Truncation of power law behavior in “scale-free” network models due to information filtering, Phys. Rev. Lett. (2002) 88, 138701.
[94] Lipsitz LA and Goldberger AL, Loss of ‘Complexity’ and Aging Potential Applications of Fractals and Chaos Theory to Senescence, JAMA (1992) 267, 1806-1808.
[95] Song C, Havlin S, Makse HA, Self-similarity of complex networks, Nature (2005) 433, 392-395.
[96] Liljeros F, Edling CR, Amaral LAN, Stanley HE, Åberg Y, The web of human sexual contacts. Nature (2001) 411, 907-908.
[97] Albert R, Jeong H, Barabási AL, Error and attack tolerance of complex networks, Nature (2000) 406, 378-382.
[98] Tachimori Y, Iwanaga H, Tahara T, The networks from medical knowledge and clinical practice have small-world, scale-free, and hierarchical features, Physica A 392 (2013) 6084-6089.
[99] Tachimori Y, Network analysis of medical knowledge to investigate the structure of medical service: Toward a mathematical approach to medical service, Ph. D. Thesis (2015 Hokkaido Univ.).
[100] 丸田俊彦 痛みの心理学 中公新書 1989
[101] 今井むつみ ことばの発達の謎を解く (ちくまプリマ―新書) 筑摩書房 2013
[102] 今井むつみ 針生悦子 言葉をおぼえるしくみ -母語から外国語まで (ちくま学芸文庫) 筑摩書房 2014
[103] Cancho RF, Solé RV, Köhler R, Patterns in syntactic dependency networks, Phys. Rev. E 69 (2004) 051915.
[104] Cancho RF, Solé RV, Least effort and the origins of scaling in human language, PNAS (2003)100, 788-791.
[105] Cancho RF, Solé RV, The small-world of human language, Proc. R. Soc. Lond. (2001) B 268, 2261-2266.
[106] Markošová M, Network model of human language, Physica A 387 (2008) 661-666.
[107] Motter AE, Moura APS, Lai YC, Dasgupta P, Topology of the conceptual network oflanguage, Phys. Rev. E (2010) 65, 065102(R).
[108] Solé R, Syntax for free?, Nature (2005) 434, 289.
[109] Solé RV, Murtra BC, Valverde S, Steels L, Language networks: their structure, function and evolution, Complexity (2010) 15, 20-26.
[110] 福井次矢、黒河清 訳「ハリソン 内科学 原著第15 版」メディカル・サイエンス・インターナショナル 2003
[111] Newman MEJ, Fast algorithm for detecting community structure in networks, Phys. Rev. E (2004) 69, 066133.
付録
1 力学系としての微分方程式
力学系とは「現在の状態から将来を予測する式」と考えられる。
\begin{eqnarray}
x_{n+1}=f(x_n) \tag{Ⅲ-付-1}
\end{eqnarray}
という式は現在の状態 \(x_n\) から時刻 \(n+1\) の状態 \(x_{n+1}\) を予測する式である。この式は時間が飛び飛びな場合であるが、時間が連続36な場合は将来を予測する式がどのようになるかが問題である。時間が飛び飛びでない場合には、ある時刻の次の時刻というものは存在しない。そこで、将来の予測に使うために微分方程式という考えが出てきた。
まず、今後は時間を表すのに \(n\) の代わりに \(t\) を使い、\(x_n\) や \(y_n\) の代わりに \(x(t)\) 、\(y(t)\) と表現する37。現在の時刻を \(t\) として将来を予想することを考える。このtは実数なので将来といっても次の将来と言うものは存在しない。いま \(h\) を小さな実数とすると、\(h\) 後の時間は \(t+h\) と表される。ここで、\(h\) はどんなに小さくても良い。今、現在の状態 \(x(t)\) を使って、将来の状態 \(x(t+h)\) を表現しようとしてみよう。将来を表現するということは、言い換えれば、将来の状態 \(x(t+h)\) と \(x(t)\) との差を表現しても良い。
すなわち
\begin{eqnarray}
x(t+h)-x(t)=f(x(t)) \tag{Ⅲ-付-2}
\end{eqnarray}
と表現できないかと考える。さて、どんな \(h\) に対しても \(h\) と関係ない、右辺の表現と言うのはありうるであろうか。この \(h\) は何でも良いのであるから、\(h\) はどんなに小さくても良い。そこで、(Ⅲ-付-2)の左辺のhをどんどん小さくしてみよう。容易に想像がつくように \(h\) を小さくすると当然 \(x(t+h)\) は \(x(t)\) に近づいていくであろう。ということは(Ⅲ-付-2)の左辺はゼロに近づくということである。十分小さい \(h\) に対して、左辺はほぼゼロ。(Ⅲ-付-2)の右辺を現在の \(x\) の値で表現しようと言うのであるから、\(h\) には関係ない。ということは \(h\) が充分小さいときの値と同じである必要がある。十分小さい \(h\) に対して(Ⅲ-付-2)の左辺はほぼゼロなのだから、右辺の \(f(x(t))\) もゼロでなければならない。このことは(Ⅲ-付-2)のような表現で将来を予想できないということである(この点が離散的すなわち時間が飛び飛びな場合との大きな違いである)。
では、どうするかである。昔の天才はその答を見つけた。(Ⅲ-付-2)の左辺を \(h\) で割ったらどうなるかと考えた。この \(h\) で割るというのは、もし、\(x(t)\) が時刻 \(t\) での位置を表すとすると、\(h\) で割った値
\begin{eqnarray}
\displaystyle\frac{x(t+h)-x(t)}{h} \tag{Ⅲ-付-3}
\end{eqnarray}
は速度(正確には時刻tと \(t+h\) の間の平均速度)になる。この値は(Ⅲ-付-2)とは違って \(h\) が小さくなっても一定のゼロではない値になることがある(ゼロになるというのは止まっている物体であるという意味である)。もし一定の値になるならば、この式で将来が予想できるのではないかと言う発想である。
微分方程式と言うのは次のような式のことである。
\begin{eqnarray}
\displaystyle\frac{dx}{dt}=ax+b \tag{Ⅲ-付-4}
\end{eqnarray}
変数が2つの場合は、
\begin{eqnarray}
\cases{\displaystyle\frac{dx}{dt} =ax+by \\ \displaystyle\frac{dy}{dt}=cx+dy} \tag{Ⅲ-付-5}
\end{eqnarray}
となる。ここで、\(a, b, c, d\) は普通の数(定数)である。しかし、一般には右辺は \(x\) や \(y\) についてのどんな式(関数)でもかまわない(例えば \(x^2\) 、\(sin(x)\) など)。そこで、一般には
\begin{eqnarray}
\displaystyle\frac{dx}{dt}=f(x) \tag{Ⅲ-付-6}
\end{eqnarray}
となる。また、\(x\) は正確に書くと \(x(t)\)、\(y\) は \(y(t)\)のことであるが、式が汚くなるので普通は \(t\) を省略して \(x\) と書いている。
ここで、左辺の定義を書くと次のようになる38。
\begin{eqnarray}
\frac{dx}{dt}=\lim_{h \to 0}\frac{x(t+h)-x(t)}{h}
\end{eqnarray}
ここで、\(\lim\)とは極限の意味である。小さな値 \(h\) をどんどんゼロに近づけていった時に近づいていく関数が \(\frac{dx}{dt}\) である。本来は極限を取るのであるが、ここで \(h\) を固定する(\(\lim\)を除いてしまう)と、\(\frac{x(t+h)-x(t)}{h}\) となる。本来は \(h\) をどんどん小さくするのであるが、十分小さい \(h\) であれば、固定しても極限の値とあまり違わないであろう。そで、例えば \(h=0.01\)(秒)であると決めてしまう。そうすると(Ⅲ-付-6)式は
\begin{eqnarray}
\frac{x(t+h)-x(t)}{h}=f(x) \quad h=0.01 \tag{Ⅲ-付-7}
\end{eqnarray}
となる。このように置き換えてしまうと、微分方程式は離散的な式(Ⅲ-付-1)と本質的に同じになる。
少し(Ⅲ-付-7)式を変形してみる。両辺にhを掛けると
\begin{eqnarray}
x(t+h)-x(t)=hf(x)
\end{eqnarray}
さらに、
\begin{eqnarray}
x(t+h)=x(t)+hf(x) \tag{Ⅲ-付-8}
\end{eqnarray}
となる。この(Ⅲ-付-8)式は、\(n\) を \(t\) 、\(n+1\) と \(t+h\) と考えれば、式(Ⅲ-付-1)とほぼ同じである。
式(Ⅲ-付-8)は現在の \(x\) の値 \((x(t))\) でもって、将来である \(t+h\) の時点での \(x\) を表している(予測している)。これは正に(Ⅲ-付-1)と同じである。この式により、現在の値によってちょっと先(\(h=0.01\) 秒先)の値 \((x(t+h))\)が分かる。さらに、これを繰り返すとずっと先の値もわかることになる。
具体的な次の方程式
\begin{eqnarray}
\frac{dx}{dt}=2x \tag{Ⅲ-付-9}
\end{eqnarray}
で考えてみる。最初の時刻(\(t=0\))の時に、\(x=1\) とする。この時、1秒後の \(x\) の値がどうなるかを考える。ここで、\(h=0.01\) としてみる。すると式(Ⅲ-付-9)は(Ⅲ-付-8)式のように変形すると
\begin{eqnarray}
x(t+h)=x(t)+h2x
\end{eqnarray}
となる。具体的な数字を入れると(\(t=0, h=0.01, x(0)=1\))
\(x(0.01)=x(0)+0.01×2×x(0)=1+0.02=1.02\)
となる。同様に0.02秒後は
\(x(0.02)=x(0.01)+0.01×2×x(0.01)=1.02+0.01×2×1.02=1.0404\)
以下同様になる。
\(x(0.03)=x(0.02)+0.01×2×x(0.02)=1.0404+0.01×2×1.0404=1.061208\)
\( \cdots \)
\(x(1)=x(0.99)+0.01×2×x(0.99)\)
\(=7.10259423358087+0.01×2×7.10259423358087=7.24464611825249\)
となり、1秒後の \(x\) の値が分かる。以下同様にして、1000回計算すれば10秒後、10000回計算すれば、100秒後の値が分かる。1時間後でも2時間後でも1年後でも計算さえすれば分かるということである。手計算では大変であるが、コンピュータであればすぐにできる計算である。
これを応用すれば、どんな微分方程式でも解けることになる。厳密には少し問題があるが、基本的には微分方程式は中学生でも解けるということになる39。
ここで、いくつか問題がある。まず、「\(h\) を適当に0.01と決めたが、そんなことをしてよいか」というものである。本当は良くはない。何でも良いのなら、もともとの定義で極限とかは出てこないであろう。極限ではなくて \(h\) を具体的な数に決めてしまうと、極限をとった場合と少し解が異なる。完全な解を求めるには \(h\) をどんどん小さくしていかなければならない。\(h\) を小さくしていくとだんだん本当の解に近づく。ですから、ある程度hを小さくしておけば、本当の解に非常に近くなり実用上は問題がなくなると思われる。では、具体的に \(h\) はどのような値にすればよいのかという問題があるが、その答えは無い。経験的には、\(h\) を少しずつ小さくして、答が実用上変化しなくなれば、それでよいと判断する40。
ところで、普通、微分方程式というのは高等数学の部類に入る。ここまでの説明ではまるで微分方程式というのは中学生でも解ける程度のものと思われるかもしれない。そこで、最後に数学ではいったい何をしているかを簡単に述べておく。まず、数学で微分方程式を解く場合は、先ほどの例
\begin{eqnarray}
\frac{dx}{dt}=2x
\end{eqnarray}
の場合は、具体的な数字を求めるのではなくて \(x\) を \(t\) の関数として求める。
この微分方程式の解は関数で書くと
\begin{eqnarray}
x(t)=Ae^{2t} \qquad Aは任意の定数
\end{eqnarray}
となる。数学ではこのような関数形を求めて、さらにこれ以外に答が無いことを証明したりしている。
そのほかに、「微分方程式にそもそも答があるのか。答があるとしていくつあるのか、答えは一意に決まるのか」などの問題を理論的に研究している。実はそのような理論的な研究があるので、ここでやっているような数値での計算の正しさが保証されている。そのような数学的な研究は非常に難解である。しかし、微分方程式の基本的な考え方、あるいは元々の発想は割りと簡単なのである。知ってもらいたいのは、その基本の発想である。
さて、(Ⅲ-付-1)のような変化方程式、もしくは(Ⅲ-付-4)、(Ⅲ-付-5)のような微分方程式を力学系と呼んでいる。もともと、力学系という言葉はニュートンの力学から出ている。ニュートンが粒子や天体の運動を表すのに初めて微分方程式を使った 。それで、そのようなタイプの微分方程式を力学系と呼んでいる。微分方程式の解が一意であるということから、現在の状態がわかれば将来がすべてわかるという決定論が生まれた。デカルトは要素還元主義を唱えたが、そこには決定論という考えは無い。決定論はニュートンの運動方程式から生れた考え方である。力学系はもともと物理の力学であったが、今では物理以外に経済学、生物学(数理生態学)などあらゆる方面で使われており、対象を記述する(研究する)ための最も有力な方法となっている。
2 相空間とアトラクター
2-1 相空間(phase space)
相空間とは、例えば複数の変数から成る力学系(微分方程式、あるいは回帰式で表される離散力学系)がある場合、その複数の変数を座標軸とする空間のことである。この力学系の運動(変化)をこの空間の軌道として表すことが出来る。また、この相空間上に表された軌道を相図と呼ぶこともある。
直線状を動く粒子の運動は力学ではその粒子の位置と速度に関する力学系(微分方程式)で表される。そのためこの運動の相空間は位置と速度を二つの座標とする平面である。例えば、バネで引っ張られている粒子の運動は次のような方程式であらわされる。
\begin{eqnarray}
\cases{\displaystyle\frac{dx}{dt} =y \\ \displaystyle\frac{dy}{dt}=-x} \tag{Ⅲ-付-10}
\end{eqnarray}
ここで、\(x\) は位置、\(y\) を粒子の速度を表している。この方程式を解くと座標 \(x\) は \(x=\sin(t)\)、速度が \(y=\cos(t)\)と時間 \(t\) の関数として表される(図Ⅲ-付-1A)。各時点での位置を \(x\) 座標、速度を \(y\) 座標に表したものが相図である(図Ⅲ-付-1B)。
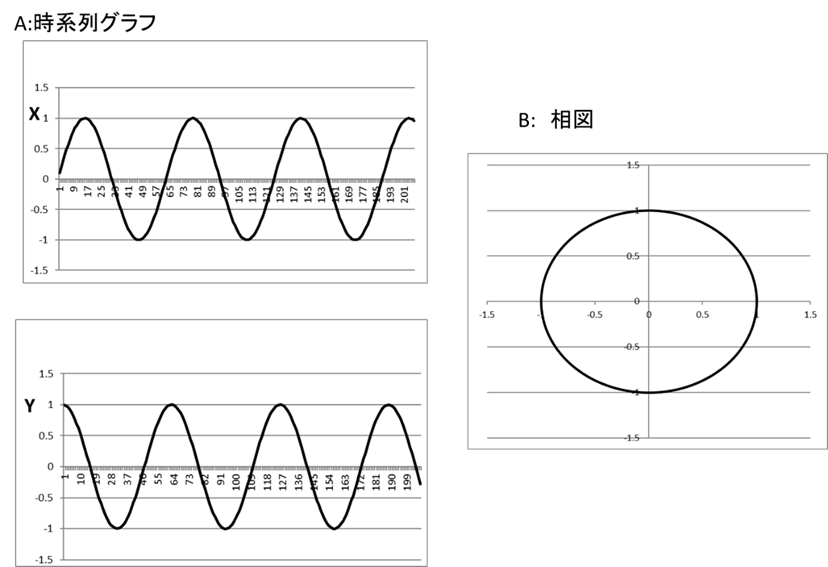
力学系を表す方程式が2つの変数で表されていれば、平面の図(2次元相空間)に、3つの変数で表されていれば3次元の図(3次元相空間)になる。変数の数は対象によっていくつでもよいので、相空間も4次元、5次元と変数の数だけの次元をもっている。また、この相空間の次元を力学系の自由度と呼んでいる。
図Ⅲ-付-2はレスラーのカオスと呼ばれている力学系を表している。
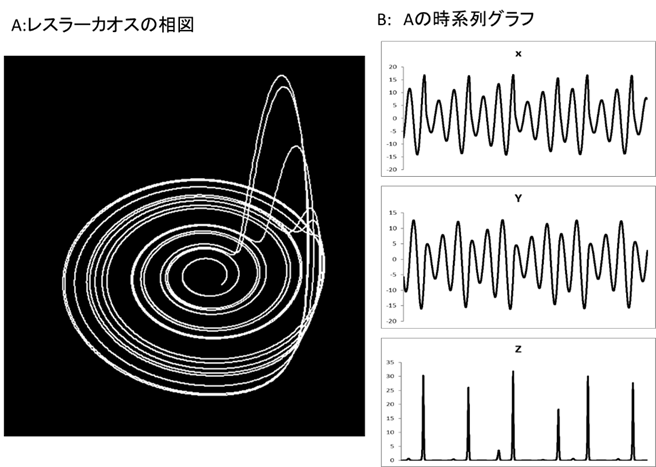
Aが相空間上の軌道、Bが各変数の時間変化のグラフである。各変数の時間変化は非常に複雑で規則性などは無いように見えるが、それを相空間上に表すとAの図のように美しい図形が浮かび上がる。一見、規則性が見えないと思われるものでも表し方を変えると規則性が見えてくる例である。一般にカオスと呼ばれる現象は相空間に表すと非常に美しい図形が浮かび上がってくる。
2-2 アトラクター
本文で述べたように、線形の力学系では最終的な安定な状態は一点である。図Ⅲ-付-3はある2次元の線形力学系(微分方程式)の解を相空間に表した図である。
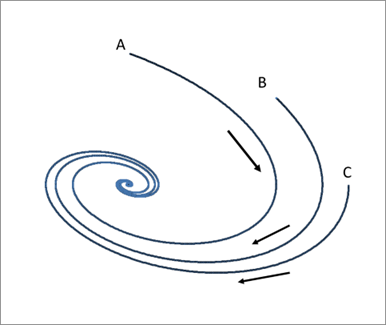
この図では3つの出発点(図上のA、B、C)から出発した3つの軌道が描いてある。3つの点は異なっているが時間がたつに従い最終的には点 \(S\) に近付いていく。実はこの力学系では平面のどこから出発しても最終状態は点 \(S\) である。すべての点からこの点へ近づいていくということは、見方を変えればこの点 \(S\) が他の点を引き込むとも考えることもできる。その意味でこのような点(一般には点の集まった図形)をアトラクター(attractor 引き込むもの)と呼んでいる。
線形力学系ではアトラクターは一点から成る。すなわち、線形力学系の最終状態は一点の固定した状態である。しかし、非線形力学系では異なっている。図Ⅲ-付-4を見てもらいたい。
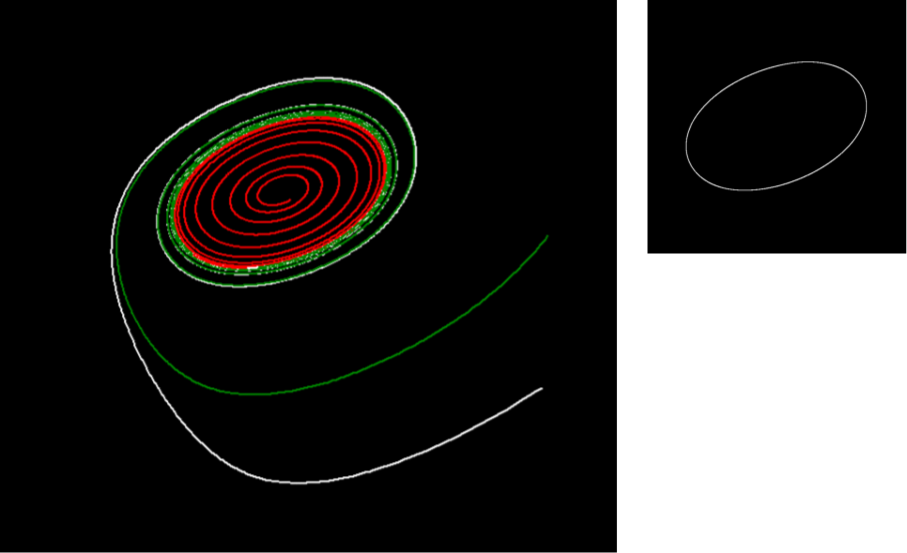
この図は2次元のある非線形力学系の相図である。図では白、赤、緑の曲線が見られる。この3つの曲線はそれぞれ異なった初期値から出発している。しかし、最終的には全ての曲線が楕円のような曲線(その部分のみ右側に図示した)に巻きついていくのがわかるであろう。白と緑の曲線は外側から巻きついていき、赤の曲線は内側から巻きついていく。最終的には楕円様の曲線上を永久に回り続ける。この楕円様の曲線(閉じているので閉曲線)のことをリミットサイクルと呼んでいる。このように、非線形力学系では最終状態が固定した点ではなくいつまでも周期運動を続ける動き続ける状態に近付いて行く場合があるのである。このリミットサイクルは前と同様に周りの点を引き込んでいくのでアトラクターの一種である。
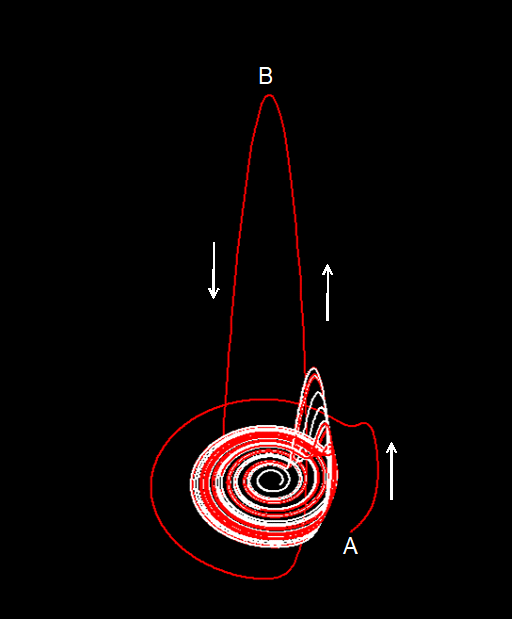
図Ⅲ-付-5は前述したレスラーのカオスである。これは、3次元の非線形力学系である。図Ⅲ-付-2(A)では今回の図の真ん中の塊(図では白い曲線)だけを表していたが、図Ⅲ-付-5ではこの塊から離れた点Aから出発したときにどうなるかを示している。図の赤い曲線に注目してもらいたい。図を見ればわかるようにAから出発した点は塊の周りをまわって、一度は遠く離れる(B点)が、その後急激に方向を変えて最終的には塊に吸収されてしまう。吸収された後はこの塊の中で永久に動き続ける。この塊は前のリミットサイクルなどと同様に周りの点を引き込んでいる。すなわち、この塊もアトラクターなのである。ただ、このアトラクターは線形の時の一点や先のリミットサイクルなどに比べて非常に複雑で奇妙な形をしている。そのためこの奇妙な形をしたアトラクターのことをストレンジアトラクターと呼んでいる。ストレンジアトラクターはカオスの特徴である。
3 ロジスティックマップ
ロジスティックマップとは以下の方程式で表される力学系である。
\begin{eqnarray}
x_{n+1}=ax_{n}(1-x_{n}) \tag{Ⅲ-付-11}
\end{eqnarray}
この方程式は \(a\) の値によってその解の性質が大きく変化する。そして、\(3.569945\ldots \lt a \lt 4\) でカオスが発生する。図Ⅲ-付-6は \(a=3.8\) の時のグラフである。
点線のAは初期条件 \(x_1=0.1\) 、実線のBは初期条件 \(x_1=0.101\) の場合のグラフである。
二つの曲線は最初ほとんど同じであるが \(n=10\) あたりから二つの曲線はずれはじめ、\(n=15\) あたり以後は二つの曲線はまるで別々の動きをしている。これが、カオスの特徴である、初期時鋭敏性である。すなわち、初期値がほとんど同じ(\(0.1\)と\(0.01\))であっても、時間がたつと二つの運動が大きく離れていく。
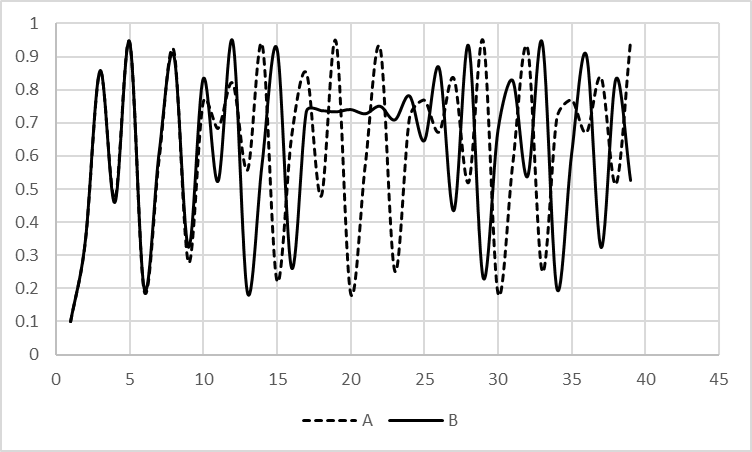
なお、\(y_{n+1}=1-ry_{n}^2\) もロジスティックマップを呼ばれ、上記の式と同様カオスを示す。この場合、上記の式で、\(r=\frac{a(a-2)}{4}, x=\frac{4(y-2)}{(a-2)}\) とすれば互いに同じものとなる。ただし、この場合には \(1.4011\ldots \lt r \lt 2\) でカオスを示す。
4 頻度分布を表す3つの表現
4-1 分布の3つの表現
A.Size – Frequency plot (サイズ – 頻度プロット:図Ⅲ-付-7A)
これは、普通の頻度分布である。横軸にサイズ(測定した大きさ)を縦軸に頻度を書いたものである。ヒストグラムと同じものである。確率密度関数 \(p(x)\) と本質的には同じものである。文章内の単語の頻度の場合は、その文章の中で同じ発生頻度をもつ単語の数(種類)を頻度に対してプロットしたものである。病名頻度分布の場合も同じように、横軸に発生頻度、縦軸にその発生頻度を持つ病名の数(頻度)をプロットしたものである。
べき分布の場合は、サイズ \(x\) を持つ対象の頻度 \(f(x)\) は次のように表される。
\begin{eqnarray}
f(x)=\frac{B}{X^{\alpha}} \quad \tag{Ⅲ-付-12}
\end{eqnarray}
ここで、\(B\) と \(\alpha\) は定数である。対象の総数が \(T\) の場合には、\(p(x)=f(x)/T\) となる。この \(\alpha\) を「べき指数」と呼んでいる。
B.Rank – Size plot (順位 – サイズプロット:図Ⅲ-付-7B)
これは、Zipfプロットとも呼んでいる。順番の付いたデータ(サイズ、頻度など何を順番の基準にしてもよい。その基準のことをここでsizeと呼んでいる)の順番(rank)を横軸にそのサイズを縦軸にしたグラフのこと。単語の頻度順、病名の頻度順、岩石を叩き割ったときにその大きさの順番、グラフ(ネットワーク)のedgeの多い順に並べたnodeなどいろいろある。
ただ、単語や病名の頻度の場合は、sizeは頻度である(ある病名の頻度がその病名のsizeになる)ので、rank-frequency plot と呼んでいる。
べき分布をするような対象では、\(n\) 番目の対象のサイズ \(S_n\) は次のように表される。
\begin{eqnarray}
S_n=\frac{A}{n^{\zeta}} \tag{Ⅲ-付-13}
\end{eqnarray}
ここで、\(A\)、\(\zeta\) は定数である。特に \(\zeta\) のことをZipf指数と呼んでいる。
C.相補累積分布関数(CCDF: Complementary Cumulative Distribution Function)と
相補累積プロット(complementary cumulative frequency plot:図Ⅲ-付-7C)
確率変数41Xの相補累積分布関数(CCDF)というのは、次のように定義されている。
\begin{eqnarray}
P(x)=Pr (X \geq x)
\end{eqnarray}
普通の言葉でいえば、ある事象の値がある値 \(x\) 以上である確率という意味である。
べき分布の場合には、\(P(x)\) は次の様に表される。
\begin{eqnarray}
P(x)=Pr(X \geq x)= \int_{0}^{\infty} p(t)dt=\frac{D}{x^{\beta}} \tag{Ⅲ-付-14}
\end{eqnarray}
ここで、\(D\)、\(\beta\) は定数であり、\(\beta = \alpha -1\) の関係がある。
さらに、\(\alpha\) と \(\zeta\) には次の関係がある。
\begin{eqnarray}
\alpha = \frac{\zeta +1}{\zeta} \tag{Ⅲ-付-15}
\end{eqnarray}
このように、ベキ分布をすると思われるデータをどの表現で表しても、ベキ指数 \(\alpha\) を求めることはできる。
4-2 ベキ指数の評価
データの集合は上記で示したように三つのタイプのプロットで表現することができる。もし、考えているデータ集合が「べき分布」に従うとすれば、上記の3つのタイプのプロットを両対数スケールで表示すれば、ほぼ直線になり、その傾きにより「べき指数」\(\alpha\) を見積もることができる。三つのプロットのどれを使っても \(\alpha\) を推定することはできるが、実際上はCCDFが最も正確な値を推定できる。
図Ⅲ-付-7は同じデータから描いた三つのタイプのプロットである。表Ⅲ-付-1はこれら三つのプロットを回帰分析した値である。これらの結果からsize – frequency plotから求めた傾きと\(\alpha\) は他のプロットからの推定に比べて大きな分散を持っているのが分かる。実際、Newmanはsize – frequency plotから求めた \(\alpha\) は他のプロットに比べて不正確であると述べている[111]。
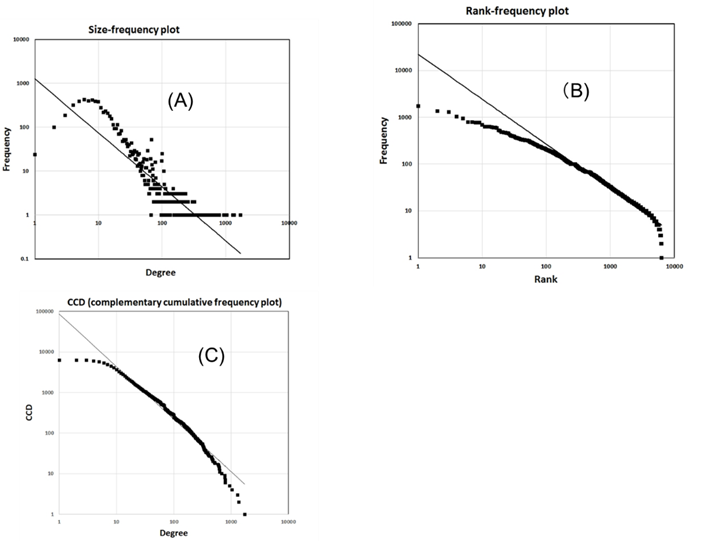
(A)頻度分布
(B)Zipfプロット
(C)相補累積分布関数
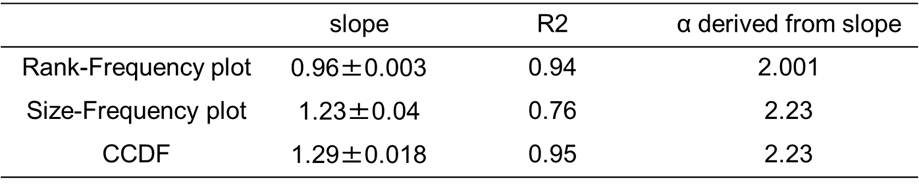
R2:決定係数
5 必要病名数
5-1 ベキ分布のときの必要病名数
病名の頻度分布が
\begin{eqnarray}
f(x)=\frac{A}{x^{\alpha}}
\end{eqnarray}
で与えられているとする。この時、病名の頻度は整数であるので、意味を持つのは \(f(x) \geqq 1\) の部分だけである。すなわち、\(A\) を決めると、その時に使える病名の数は \(f(a) \geqq 1\) となる最大の \(a\) で決まる。
そしてその時、 病名付け可能な患者数 \(s\) は次のようになる。
\begin{eqnarray}
s=\sum_{k=1}^{a}\left[\frac{A}{x^{\alpha}}\right] \approx \int_{1}^{a} \frac{A}{x^{\alpha}} dx \tag{Ⅲ-付-16}
\end{eqnarray}
これを計算する。
\(\alpha \gt 1\) の場合は
\begin{eqnarray}
s=\left[-\frac{A}{\alpha-1}x^{-\alpha +1}\right]_1^{a}=\frac{A}{\alpha-1}(1-a^{})
\end{eqnarray}
ここで、\(\frac{A}{a^{\alpha}} =1\) だから、\(A=a^{\alpha}\) を代入すると \(s=\frac{1}{\alpha-1}(a^{\alpha}-a) \approx \frac{a^{\alpha}}{\alpha-1}\) となる。\(a\) について解くと、
\begin{eqnarray}
a=\sqrt[\alpha]{(\alpha-1)s} \tag{Ⅲ-付-17}
\end{eqnarray}
これは患者数 \(s\) に病名をつけるときに必要な病名数が \(a\) であることを示している。
\(\alpha=1\) の場合は同様にして
\begin{eqnarray}
s=\left[A\log{x}\right]_{1}^{a}=A\log{a}=a\log{a} \tag{Ⅲ-付-18}
\end{eqnarray}
5-2 指数分布の場合の必要病名数
\(f(x)=A\exp(-bx)\) の場合
ベキ分布と同様に
\begin{eqnarray}
s=\sum_{k=1}^{a}A\exp{(-bn)} \approx \int_{1}^{a}A\exp{(-bx)}dx \tag{Ⅲ-付-19}
\end{eqnarray}
で近似する。ただし、\(A\exp{(-ba)}=1\) であるので、\(A=\exp{(ba)}\) もしくは、\(a=\log{\frac{A}{b}}\) である。
積分を実行すれば
\begin{eqnarray}
s=\left[-\frac{A}{b}\exp{(-bx)}\right]_{1}^{a} = \frac{A}{b}\exp{(-b)}-\frac{A}{b}\exp{(-ba)}
\end{eqnarray}
となる。\(A=\exp{(ba)}\) だから、\(ab=\log{A}\) となる。これを代入して
\begin{eqnarray}
s=\frac{1}{b}\left(\frac{e^{ba}}{e^{b}}-1 \right) \approx \frac{e^{b(a-1)}}{b}
\end{eqnarray}
\(a\) について解けば
\begin{eqnarray}
a=\frac{\log{bs}+b}{b} \tag{Ⅲ-付-20}
\end{eqnarray}
となる。\(b\) は実測値と適当にあわせる。
例えば、\(b=0.05\) ならば、\(s=1000\) で \(a=80\) となる。 1000人に病名を付けるには80個の病名があればよい。 大体、これぐらいで実測データに合う。結果のグラフは本文の図Ⅲ-3-13を参照されたい。
