PHYSIOLOGICAL SIGNIFICANCE OF THE SHIL’NIKOV PHENOMENON IN THE FOCAL ACCOMMODATION SYSTEM OF HUMAN EYES

TAKEO SUMIDA,  TAKASHI TAHARA, HIROAKI IWANAGA

International Journal of Bifurcation and Chaos, Vol. 4, No. 1 (1994) 231-236

We found the Shil’nikov phenomenon in the focal accommodation system of human eyes. The attractors changed forme and the dynamics shifted to being periodic on stimulating the autonomic nervous system. This chaos potentially suggests that one can qualitatively grasp the state of the autonomic nervous system which innervates these systems.

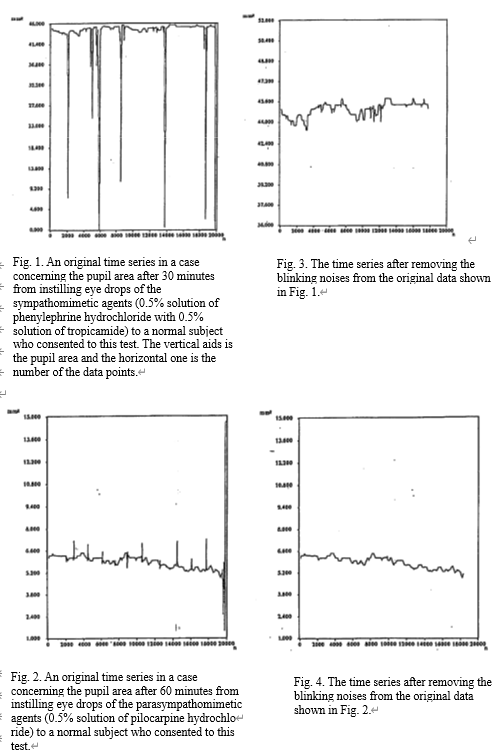
The muscular movements affecting the thickness of the lens and the size of the pupil in human eyes are controlled by the autonomic nervous system [Thompson & Robert, 1987]. In these movements, fluctuations are observed even in steady viewing conditions [Campell et al, 1959]. We measured these fluctuations and reconstructed the dynamics. Furthermore, we investigated the relationship between the dynamics and the autonomic nervous system. We arranged for forty normal subjects, aged 22-63 years, to view a target fixed at a far point under steady viewing conditions. Then, we measured simultaneously the time series of a single variable of the refractive power of the lens in the direction of 180 degrees and that of the pupil area by an optometer using infrared rays (MODEL AR3-SA14, Nidec Co. Ltd.) and an iriscorder (MODEL IC11OO, Nidec Co. Ltd.), The sampling interval was 5 msec. Sampling time was for 100 sec. Furthermore, instilled eye drops of sympathomimetic agents and parasympathomimetic agents, respectively to five normal subjects who consented to this test and measured the time series of them after 10, 30, 60, and 120 minutes as in Figs. 1 and 2. The sympathomimetic agent was a 0.5% solution of phenylephrine hydrochloride with a 0.5% solution of tropicamide. The parasympathomimetic agent was a 1% solution of pilocarpine hydrochloride. After removing the noises of blinking from these time series, as in Figs. 3 and 4, the attractors were reconstructed by adopting the embedding method [Packard et al., 1980; TsOcens, 1981]. Our data was embedded into a four-dimensional phase space, because we calculated the correlation dimension [Grassberger & Procaccia, 1983a, 1983b] and estimated that the dynamics was at most four-dimensional. However, the obtained attractors were nonuniform. Furthermore, it is inappropriate to measure the time series for a long time because of the difficulty of keeping its stationarify. Therefore, it is practically difficult to estimate the proper dimension of our attractors from the limited data points [Tsuda et al., 1992]. Furthermore, we projected the attractors into three-dimensional phase space by taking the parallel projection of supposed four-dimensional objects (Miyazaki & Ishihara [1989]; see also Tsuda et al [1992]). We calculated the Lyapunov exponents by the Wolf method [Wolf et al., 1985] with slight modifications, because at least for the largest Lyapunov exponent, this method had indicated reliable results in the case of human capillary vessels (see also Tsuda et al. [1992]). In general, it is difficult to prove deterministic chaos in the experimental data obtained from biological systems. However, the estimation of the largest Lyapunov exponent is relatively reliable. We adopted the Lyapunov exponent as a practical measure of deterministic chaos (see also Tsuda et al. [1992]). The reconstruction of the attractors and the calculation of the Lyapunov exponents were computed by an engineering workstation (MODEL NWS-3865, Sony Co. Ltd.). As a result, the attractors projected into three-dimensional phase space looked like a form of the Shil’nikov type (Shil’nikov phenomenon) [Shil’nikov, 1965; Broer & Vegter, 1984; Arneodo et al, 1981] as in Figs. 5-7. The reason is as follows. We observed that the trajectory started from a pole close to the other pole through the sphere with spiral motions and came back again near one pole with spiral motions on the surface of the sphere, or observed the reverse motions.

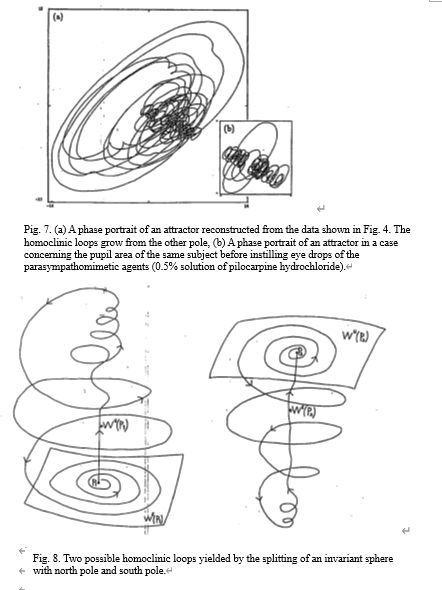
In three-dimensional flow, the coincidence of two two-dimensional manifolds (one stable, the other unstable) at two spiral saddles becomes an invariant sphere with a north pole and a south pole. The coincidence is exceptional. When the split between them occurs, the branch of W^u(P₁) in the sphere comes down to W^s(P₁), or one of W^s(P₂) in the sphere goes to W^u(P₂) as in Figs. 8 and 9. Then, transverse intersections are yielded [Guckenheimer & Holmes, 1990; Wiggins, 1992].  [P₁ denotes a saddle focus fixed point with a two-dimensional stable manifold and a one-dimensional unstable manifold, P₂ denotes a saddle focus fixed point with a one-dimensional stable manifold and a two-dimensional unstable manifold, and W^u(P_i) denotes an unstable manifold, W^s(P_i)  denotes a stable manifold at P_ii i = 1, 2]. Broer and Vegter had mathematically proved that the split yielded a Shil’nikov phenomenon (see also Broer & Vegter [1984]).

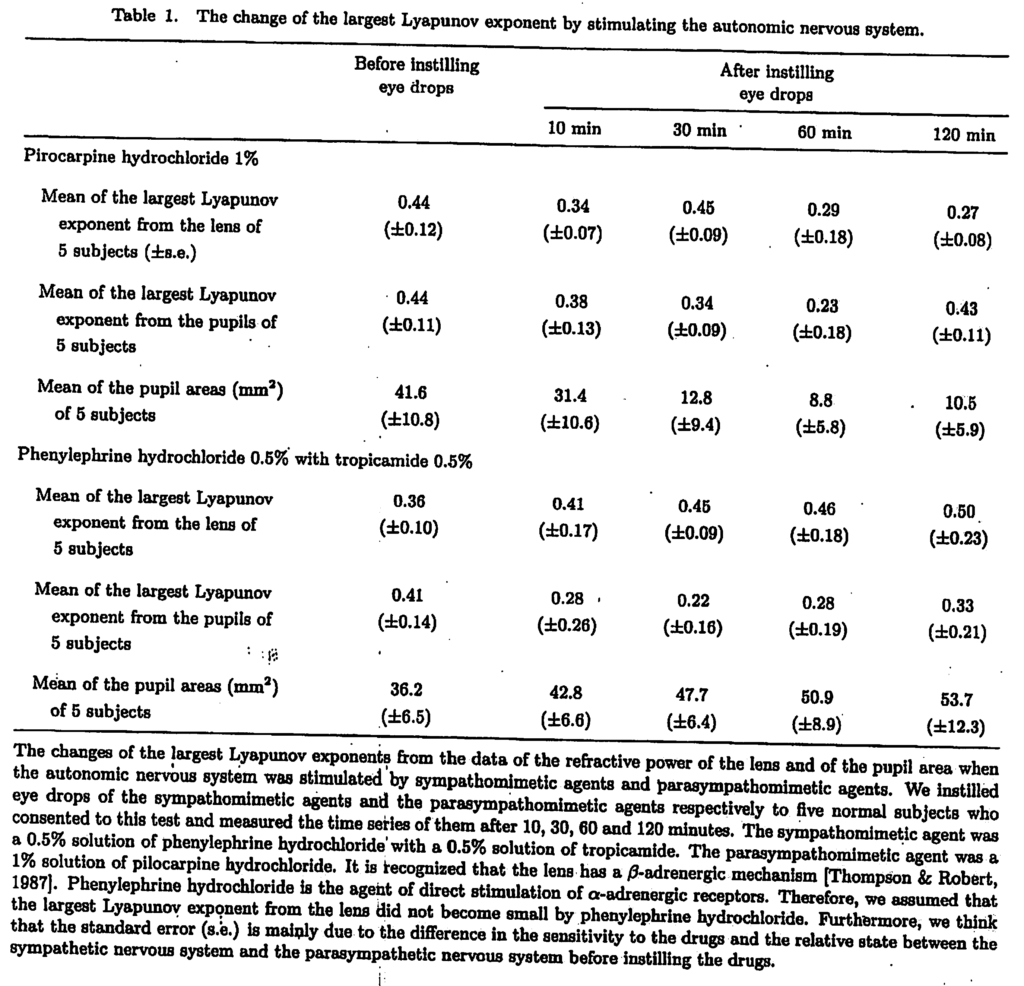
When the sympathetic nervous system is stimulated, the orbits of the attractors are attracted to one pole, as in Fig. 6(a). On the contrary, when the parasympathetic nervous system was stimulated, the orbits were attracted to the other pole as in Fig. 7(a). The two poles existed independently of embedding dimension 4 or 3. The largest Lyapunov exponents from forty normal subjects were positive (lens: mean = 0.50, max.= 0.86, min. = 0.23, and standard deviation = 0.17; pupil: mean = 0.46, max. = 0.71, min. = 0.26, and standard deviation = 0.09). The second Lyapunov exponents were also positive. Furthermore, the values of the largest Lyapunov exponents became small when the attractors were strongly attracted to the poles by these stimulations, as in Table 1 [see also Fig. 6(a)].

From these facts, we concluded that the dynamics of the focal accommodation system of human eyes is deterministic chaos, which has the Shil’nikov phenomenon, and one pole of our Shil’nikov type attractor corresponded to the pole of stimulation of the sympathetic nervous system, while the other pole corresponded to the pole of stimulation of the parasympathetic nervous system. We also concluded that the largest Lyapunov exponent became small, namely the dynamics shifted to being periodic, on strong stimulation because the orbits were attracted to the local stable manifolds (see also Shil’nikov [1965] and Broer & Vegter [1984]) in the respective poles. Further investigation is required to determine which pole corresponds to the north pole and which to the south pole.

Either one or other pole generates the homoclinic loops. Determining the pole allows us to qualitatively grasp the state of the autonomic nervous system, which controls the motions (namely, which mainly controls the dynamics: the sympathetic nervous system or the parasympathetic nervous system?).

Acknowledgments

We thank Professor Ichiro Tsuda for significant advice.  One of the authors (T., S.) thanks Dr. Youtarou Matsuoka for supporting our research and Dr. Yasutaka Ogawa for useful discussions.

References

Ameodo, A., Coullet, P. & TYessetj C. [1981] “Possible new strange attractors with spiral structure,”  Commun. Math. Phys. 79, 573-579.

Broer, H. W. & Vegter, G. [1984] “Subordinate Shil’nikov bifurcations near some singularities of vector fields having low codimension,” Ergodic Theory Dynamical Systems 4, 509-525.

Campell, F., Robson, J., & Westheimer, G. [1959] “Fluctuations in accommodation under steady viewing conditions,” J. Physiol (London) 145, 579.

Qrassberger, P. & Procaccia, I. [1983a] “Characterization of strange attractors,” Phys. Rev. Lett. 50, 346-349.

Grassberger, P. & Procaccia, I. [1983b] “Measuring the strangeness of attractors,” Physica D9,189-208.

Guckenheimer, J. & Holmes, P. [1990] “Local codimension two bifurcations of flows,” in Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields (Springer-Verlag, New York) pp. 394-395.

Miyazaki. K. & Ishihara, K. [1989] Four-Dimensional Graphics-Towards High Dimensional CG (Asakura-Shoten, in Japanese).

Packard, N. H., Crutchfield, J. P., Farmer, J. D. & Shaw, R. S. [1980] “Geometry from a time series,” Phys. Rev. Lett. 45, 712-715.

Shil’nikov, L. P. [1965] “A case of the existence of a countable number of periodic motions,” Sov. Math. Dokl 6,163-166.

Takens, F. [1981] “Detecting strange attractors in turbulence,” in Lecture Notes in Mathematics, eds. Rand, D. A. & Young, L. S. 898, 366-381 (Springer-Verlag, Berlin).

Thompson, H. T. & Robert, A. M. [1987] “The pupil and the accommodation,” in Adler’s Physiology of the Eye, ed. Robert, A. M. (the C. V. Mosky Company, St. Louis) pp. 309-320.

Tsuda, I., Tahara, T. & Iwanaga, H. [1992] “Chaotic pulsation in human capillary vessels and its dependence on mental and physical conditions,” Ini. J. Bifurcation and Chaos 2(2), 313-324.

Wiggins, S. [1992] “Global bifurcations and some aspects of chaos,” in the Japanese version of Introducfton to Applied Nonlinear Dynamical Systems and Chaos (Springer-Verlag, New York, 1990) Vol. 2, 439-441 (Springer-Verlag, Tblqro).

Wolf, A., Swift, J. B., Swinney, H. L. & Vastano, J. A. [1985] “Determining Lyapunov exponents from a time series,” Physica D16, 285-317.